Espectro de los hamiltonianos magnéticos de Stark $H(\mu,\epsilon)$

Question

Estoy buscando un documento donde pueda encontrar una prueba el espectro del del Stark Magnético Hamiltonianos $H(\mu,\epsilon)=\big(D_x-\mu y)^2+D^2_y+\epsilon x+V(x,y)$ citado en el artículo siguiente para $\epsilon\not=0$ ver ecuación $(1.2)$ en

http://www.hrpub.org/download/20140105/MS6-13401691.pdf

Gracias

Answer 1

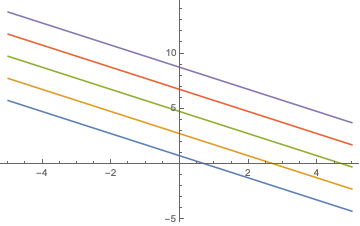
Una transformación unitaria $\tilde{H}=e^{-i\mu xy}He^{i\mu xy}$ transformará el hamiltoniano en $$\tilde{H}(\mu,\epsilon)=D_x^2+(D_y+\mu x)^2+\epsilon x+V(x,y),\;\;D_\nu=-i\partial/\partial\nu,$$ por lo que para $V\equiv 0$ se trata de un oscilador armónico con funciones propias $\psi_{k,n}(x,y)=e^{iky}\phi_n(x)$ y los valores propios $$E_n(k)=(2n+1)\mu-k\epsilon/\mu-\tfrac{1}{4}(\epsilon/\mu)^2,\;\;n=0,1,2,\ldots,\;\;k\in\mathbb{R}.$$ Este espectro se extiende desde $-\infty$ a $+\infty$ , véase el diagrama de $E_n$ frente a $k$ para $n=0,1,2,3,4$ (en $\mu=1=\epsilon$ ).

El efecto de un potencial localizado $V$ puede tenerse en cuenta en la teoría de la perturbación, no puede cambiar el rango del espectro. Por cierto, este es el espectro de un electrón en campos magnéticos y eléctricos perpendiculares.