¿Cuánta información sobre la magnitud de una cascada se puede obtener a partir de su sonido?

Question

¿Es posible limitar la altura, el flujo de volumen o la distancia de una cascada a partir del análisis cuantitativo de una grabación de alta calidad de su sonido?

Como dato adicional, los sonidos simulados de salpicaduras de líquidos o agua que se vierte han sido sintetizados por computadora. El grupo que realizó esta investigación estaba en la Universidad de Cornell. Esto parece ser un ejemplo de una solución al problema inverso. Si escuchas la simulación con los ojos cerrados, ¿puedes distinguir la cascada del grifo abierto?

Se han identificado tamaños de gotas de lluvia mediante diferentes mecanismos físicos asociados con las salpicaduras de las gotas y se han utilizado como base para pluviómetros acústicos.

Mi pregunta se refiere a cómo encontrar una solución (parcial) para el problema inverso. A partir de las mediciones de sonido, ¿cómo se podría diferenciar entre caídas muy altas y modestas, por ejemplo, comparar las Cataratas de Snoqualmie (82 m) y las Cataratas del Ángel (979 m)?

El espectro del sonido de una cascada se describe cualitativamente como 'de banda ancha' o 'ruido marrón' y aún no he encontrado un buen ejemplo de un espectro acústico real de una cascada.

Creo que la energía total del sonido radiada al aire (y al suelo) igualaría la energía gravitacional liberada por el agua que cae, menos una pequeña cantidad de energía que se convierte en calor y calienta el agua.

Me parece que los espectros de una cascada de 100 m frente a una de 1000 m podrían tener ratios predecibles diferentes de potencia de baja y alta frecuencia. ¿Existen mecanismos mecánicos de fluidos o acústicos que entren en juego para las caídas más altas que no operan a alturas más bajas? ¿Podría haber sonidos diagnósticos relacionados con la cavitación?

¿Habría demasiada reflexión y dispersión de sonido en una cuenca de cascada real como para poder realizar mediciones?

Mis Conclusiones

Bien, creo que ahora tengo una respuesta satisfactoria a mi pregunta y he otorgado la recompensa a zhermes. Creo que su respuesta describe correctamente la física subyacente del problema, y una vez que entendí eso, pude encontrar mucha más información relevante y realizar algunos cálculos preliminares bastante aproximados.

En resumen, el proceso físico importante podría ser la dispersión resonante del sonido ambiental dentro de la cascada turbulenta por 'nubes de burbujas'. Esto se conoce como resonancia de Minnaert y se ha extendido para describir 'nubes de burbujas' además de burbujas individuales de aire. Este enfoque ha sido utilizado de manera productiva para analizar el ruido de las hélices y el sonido de las olas oceánicas. Lo encontré útil para comenzar a pensar en cómo el sonido de una cascada puede verse afectado por la altura de la caída.

La frecuencia resonante de una 'nube de burbujas' es inversamente proporcional al radio de la nube. También encontré ejemplos de análisis que mostraron una dependencia ~1/f para el espectro de potencia de este tipo de ruido (como también sugirió zhermes).

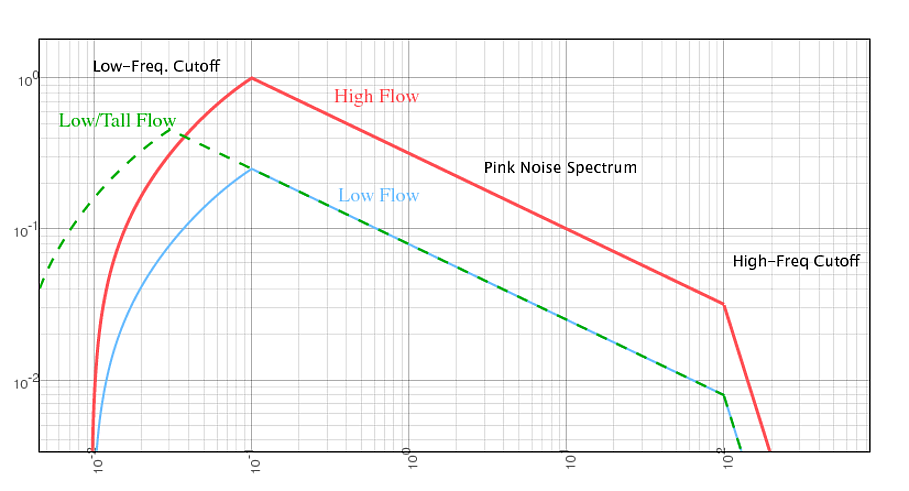
Por lo tanto, podríamos prever que la frecuencia de corte de baja frecuencia en el espectro de potencia del ruido de la cascada podría estar determinada por el tamaño máximo de las 'nubes de burbujas'.

Un (obvio) aspecto que parece ser que tiene que ser generado en la poza al pie de la cascada es el sonido que contiene información sobre la altura total. Los sonidos que se originan en el flujo a 10 metros de la cima de una catarata de 1000 m no deberían ser diferentes a los de una caída de 10 metros. Una vez que el agua cae los 990 m adicionales, también ha ganado más energía cinética que estaría disponible para generar una 'nube de burbujas' de un tamaño que depende de la altura de la cascada.

Igualando la energía gravitacional del agua en la cima de la cascada, la energía cinética del agua cuando golpea la poza y el trabajo para empujar un chorro en la poza, calculé la profundidad máxima que el chorro podría penetrar en la poza y tomé eso como el tamaño máximo de la 'nube de burbujas'. Esta estimación del tamaño de la 'nube de burbujas' es proporcional al inverso de la raíz cuadrada de la altura de la cascada.

Sustituyendo condiciones estándar para el agua y la presión, este análisis arrojó una frecuencia de corte de baja frecuencia (que también fue la frecuencia de máxima potencia) que estaba muy en el rango del infrasonido (<20 Hz) y por debajo del rango de frecuencia de la audición humana. La conclusión que se puede sacar de estos cálculos es que el tono de las cascadas altas y bajas no es muy diferente en el rango de la audición humana. Las diferencias podrían ser perceptibles para caídas que tienen grandes flujos volumétricos que son capaces de generar mucha potencia en los límites de la audición. Las diferencias también podrían percibirse (sentirse en lugar de escucharse) como infrasonido.

Quizás esto explique por qué las grabaciones MP3 de cascadas, cascadas y arroyos suenan tan similares. Podríamos estar perdiendo la información que nos llega como infrasonido.

Answer 1

Tenga en cuenta que lo siguiente es puramente conjetural. Lo ofrezco voluntariamente debido a la falta de otras respuestas después de numerosos días, el interés de la pregunta y la probable falta de personas/referencias que estén explícitamente experimentadas con este tema específico.

Imagen Básica

Como una relación general, estoy seguro de que se puede correlacionar el volumen de sonido con la energía total que se está disipando --- pero el ruido producido va a ser una fracción (virtualmente) insignificante de esa energía total (en general, el sonido lleva muy poca energía1).

A orden cero, creo que es seguro asumir que la cascada produce un ruido blanco, pero obviamente eso necesita ser modificado para ser más preciso (es decir, probablemente rosa/marrón a primer orden). Además, al considerar la transición desde una pendiente pequeña/gradual, a una cascada real, puedo convencerme de que definitivamente hay una dependencia tanto de la altura de la caída como del volumen de agua2.

¿Cómo afectaría la altura al espectro?

Por lo general, los espectros de potencia exhiben cortes de potencia de alta y baja energía en forma de ley de potencia, y esperaría lo mismo en este caso. En el régimen de baja frecuencia, si comienzas con un flujo suave antes de la cascada, no hay nada que genere perturbaciones más grandes que la escala de tamaño físico de la propia cascada. Entonces, esperaría un corte de baja energía en una longitud de onda comparable a la altura de la cascada. En otras palabras, cuanto más alta la cascada, más bajo será el ruido.

También tiene que haber un corte de alta energía, si no es por otra razón, para evitar una catástrofe ultravioleta/divergencia. Pero, ¿qué lo causaría físicamente? Presumiblemente las perturbaciones de escala más pequeña (frecuencia más alta) provienen de la turbulencia del flujo3, y serían determinadas principalmente por la viscosidad y disipación del fluido4. Generalmente, dicho espectro cae como el número de onda (frecuencia) a la potencia -5/3. Pero hay que tener en cuenta que este corte de alta frecuencia no parecería cambiar de cascada a cascada.

En general, estoy sugiriendo (léase: conjeturando) lo siguiente:

• Corte exponencial o de ley de potencia de baja frecuencia en longitudes de onda comparables con la altura de la cascada.
• Corte de ley de potencia de alta frecuencia a partir de un espectro de turbulencia de Kolmogorov, en una longitud de onda comparable a la escala de longitud viscosa.
• Estos regímenes estarían conectados por una ley de potencia de ruido rosa/marrón.
• La amplitud del sonido es directamente proporcional a algún producto de la tasa de flujo y la altura de la cascada (supongo que el término anterior dominaría).

Por ejemplo: El siguiente espectro de potencia (potencia vs. frecuencia - ambos en unidades arbitrarias).

La Respuesta

Estoy seguro de que se puede obtener información del sonido. En particular, estimaciones de su altura/tamaño, tasa de flujo, y distancia5. También estoy seguro de que esto sería bastante difícil en la práctica y, para la mayoría de los propósitos, simplemente escuchar y adivinar probablemente sería tan preciso como cualquier análisis cuantitativo ;)

---

¿Consideración adicional?

Supongo que es posible que las gotas de agua puedan generar sonido adicional en escalas comparables a su propio tamaño. Eso sería bastante genial, pero no tengo idea de cómo estimar/adivinar si eso es importante o no. Probablemente solo contribuirían al sonido en longitudes de onda comparables a su tamaño (y por lo tanto limitados por los tamaños máximos/mínimos de las gotas de agua6...).

El agua, especialmente en forma de neblina/rocío, puede ser muy efectiva para atenuar el sonido (que solían usar para el transbordador espacial). Supongo que esto tendría un efecto significativo en el sonido resultante para alturas/volúmenes de flujo en los que se produzca una neblina/rocío.

Las propiedades acústicas del paisaje también podrían ser importantes, es decir, si el paisaje es abierto (con la caída de la cascada siendo como una función escalonada) o cerrado (como si la caída fuera al final de un valle en forma de u, etc).

Finalmente, también es importante considerar las superficies adicionales involucradas: por ejemplo, rocas, la superficie en el borde del salto de la cascada, arena cerca de la base de la cascada, etc.

---

Notas al pie

1: Considere cuánto sonido produce un amplificador de 60 vatios, y suponga tal vez una eficiencia del 10% (probablemente optimista). Eso es fuerte, y lleva una pequeña cantidad de potencia en comparación con lo que una cascada de igual volumen está llevando. La gran mayoría de la energía de la cascada terminará como calor, turbulencia y movimiento en masa.

2: También supondría que la altura/volumen se mezclarían después de cierto punto de saturación (es decir, 1000 m3/min a 20 m de altura es más o menos lo mismo que 500 m3/min a 40 m de altura)... pero ignoremos eso por ahora.

3: La turbulencia tiende a transferir energía de escalas grandes a escalas pequeñas.
Vea: http://en.wikipedia.org/wiki/Turbulence

4: Descubrir la relación real para la escala de tamaño más pequeña de la turbulencia está más allá de mi alcance y, creo, está fuera de la escala de esta 'respuesta'. Pero involucra cosas como el espectro de Kolmogorov y la escala de longitud asociada.

5: La distancia podría estimarse en base a una combinación del espectro y el nivel de volumen - para desenredar la degeneración entre volumen de sonido y distancia.

6: ¿Tal vez el tamaño mínimo de las gotas de agua está determinado por su comportamiento balístico (en lugar de formar una neblina)?

Answer 2

Excelente discusión, actualmente estoy investigando pequeñas cascadas en el Reino Unido. En mi investigación hasta ahora utilizando 1/3 octavas, he encontrado que los espectros de cascadas de diversas formas son similares (y una combinación de Rosa y Blanco). Características especiales, rocas, curvatura, altura de la cabeza parecen tener un efecto considerable al igual que el ancho y el ángulo de inclinación con el que el agua impacta en la superficie aguas abajo/piscina de inmersión (ya que no todas tienen grandes piscinas de inmersión) Tengo las grabaciones de la señal y podría procesarlas posteriormente en bandas de frecuencia mucho más pequeñas.

Además de esto, los resultados del efecto del tamaño muestran que varios parámetros medidos en los sitios de campo contribuyen con efectos de tamaño grandes variables a diferentes frecuencias de manera no lineal y estocástica en algunos casos.

Hay un libro llamado "La burbuja acústica" de T Leighton que podría añadir matemáticas locas para aquellos que estén interesados; creo que las burbujas tendrán un impacto significativo en los espectros registrados desde la explosión de burbujas hasta la absorción del sonido en ciertas frecuencias.

Answer 3

Aunque no tengo la ambición de responder completamente la pregunta (no soy un experto en acústica ni en mecánica de fluidos), intentaré compartir mi punto de vista con todos. Con suerte, alguien captará la idea y podrá avanzar desde allí.

Usted sugiere determinar tres parámetros principales: altura, flujo de volumen y distancia, analizando la grabación del sonido. En primer lugar, tendrá serias dificultades para encontrar la distancia. Aunque, en un escenario perfecto, la intensidad del sonido debería seguir la ley del inverso del cuadrado con la distancia, en la práctica se verá fuertemente afectada por el terreno. Considere estar oculto detrás de una gran roca o en línea directa con la cascada, con ambas distancias siendo iguales. En el primer caso, el sonido será definitivamente notablemente más débil. El sonido probablemente también diferirá cuando esté parado en un valle estrecho o en un plano abierto.

Así que omitamos la distancia. Supongamos que tenemos un lugar cercano a varias cascadas, cada una similar y en condiciones similares. Ahora, solo nos interesa la altura y el flujo de la cascada. Estoy de acuerdo con usted en que la energía del sonido estará dada por la energía gravitacional del agua que cae, pero con algo de fricción, posible cambio en la energía cinética del agua y pérdida debido a la turbulencia del flujo. Ahora, lo primero que no estoy seguro es ¿cómo afectan estas pérdidas la altura o el flujo de la cascada? ¿Cambiarán las pérdidas de manera lineal con estos parámetros o es la relación más compleja? ¿Y hay otros factores que puedan jugar un papel?

La segunda pregunta importante es, ¿cómo afecta la altura y el flujo de la cascada al sonido de la misma? ¿Uno de ellos tiene un impacto más fuerte en el espectro que el otro? ¿O una cascada con una altura $h$ y un flujo $Q$ tiene el mismo sonido que una cascada con altura $2h$ y flujo $Q/2$? En mi ignorancia, también es posible que el espectro no se vea afectado en absoluto y suenen igual, solo con diferente intensidad.

Según mi (falta de) conocimiento, estas preguntas no pueden ser respondidas por simples predicciones teóricas y la única forma posible de encontrar una solución podría ser medir directamente el sonido de varias cascadas y compararlos. Pero como dije, no tengo habilidades en este campo y podría estar completamente equivocado.

Finalmente, en cuanto a la realización práctica, será muy difícil medir el sonido de diferentes cascadas en las mismas condiciones. El sonido se verá fuertemente afectado por la reflexión (si hay rocas por todos lados, la reflexión será más fuerte que en medio de un bosque), u otras fuentes de ruido (como el flujo de agua debajo o arriba de la cascada). Pero se podría eliminar esto en el postprocesamiento si se conocen las condiciones en las que se tomó la grabación.

Antes de terminar, recuerdo una vez más que no soy un experto en los campos de acústica o dinámica de campo y es posible que mi argumentación sea incorrecta. Pero creo que esta publicación puede iniciar una discusión que lleve a un resultado concluyente.

---

Edición: Como me señaló BrianWa en los comentarios, la altura de la cascada afectará la velocidad de las gotas que caen y esto seguramente afectará el espectro del sonido. Sin embargo, creo que este cambio solo será observable hasta una altura tal que la resistencia del aire durante la caída compense la gravedad y la gota no aumente más la velocidad. Todas las cascadas más altas que este umbral probablemente tendrán el mismo (o muy similar) espectro de sonido.

Answer 4

Yo especularía que cuanto mayor sea la caída, hasta cierto punto, más rápido se empuja hacia abajo el agua en la superficie como resultado del impacto de la cascada. Por lo tanto, puede haber un efecto Doppler dentro de la burbuja que comprime más el sonido subacuático en caídas más altas.

Si esto afecta o no lo suficiente al sonido durante el tiempo de explosión es cuestionable. Supondría que una pared superior de la burbuja que avanza más rápido crea algunos sonidos de frecuencia más alta. Pero el oído humano no puede discriminar diferentes frecuencias que están muy cerca entre sí (enmascaramiento en psicoacústica).

Por lo tanto, se tendría que realizar un análisis espectral. Analíticamente, especularía que la masa se desplaza de frecuencias más bajas a más altas, a lo largo del espectro, para caídas de agua más altas (hasta cierto límite debido a la velocidad terminal).