Detección de valores atípicos para datos sesgados

Question

Tengo un conjunto de datos como el siguiente:

4.8856
4.8914
4.9125
4.9338
4.9563
4.993
4.9947
4.9947
4.995
5.2932
4.981
4.981
4.981
4.982
4.982
4.982
4.982
4.983
4.983
4.984
4.984

Histograma

Cuando uso 3*IQR en un diagrama de caja en R para detectar valores atípicos, me muestra 10 registros de 21 como valores atípicos. Sin embargo, como puedo ver en el histograma, principalmente hay 1 valor atípico (el más a la derecha) que necesito filtrar.

¿Cuál sería el método recomendado para detectar valores atípicos en estos datos?

Answer 1

Para este tipo de datos, y cualquier otra distribución univariada, tengo estas recomendaciones.

1. Usa el contexto que tengas sobre los datos. ¿Qué se espera? ¿Qué es o sería sorprendente o alarmante?

Hay al menos cuatro situaciones aquí:

1a. Son tus datos y deberías saber cómo se produjeron y qué esperar. Por ejemplo, soy geógrafo y sé que las ciudades grandes y los ríos grandes son genuinos, pero que ninguna ciudad tiene 100 millones de habitantes ni ningún río 100,000 km de largo. Ese tipo de detalles pueden parecer triviales, pero saber lo que es imposible o implausible puede salvar un análisis de tonterías. En el extremo más fácil, un valor atípico puede ser evidentemente el resultado de algún error de cálculo o informe y corregirse o descartarse como irreparable.

1b. Eres el analista de datos y tienes un cliente, jefe u otra persona que debería conocer los datos. Inicia una conversación si aún no lo has hecho.

1c. Puedes utilizar conocimientos generales o buscar en Google u otras búsquedas simples.

1d. Ninguna de las anteriores. No deberías llegar aquí nunca, pero reconoce al menos que sin ningún contexto no estás en buena posición para juzgar.

Establezco todo lo anterior porque la idea de que puedes tomar decisiones acertadas sobre lo que es o no es un valor atípico sin conocimiento de la materia está entre ser excesivamente optimista y absurdamente necio.

Concretamente, ¿cómo procedes?

2. Siempre grafica los datos. Casi cualquier gráfico servirá siempre y cuando puedas ver los detalles de los datos, porque necesitas ver todos los datos como telón de fondo.

2a. Yudi Pawitan tiene una idea interesante: un gráfico normal de cuantiles funcionará bien incluso si estás lejos de esperar algo como una distribución normal, porque las características y patologías de cualquier tipo deben ser claras (no solo los valores atípicos, sino también la asimetría, las colas anchas, los vacíos, la granularidad, y así sucesivamente). Saber cómo se comparan tus datos con una normal es como saber tu temperatura cuando sabes que tienes fiebre. Vale la pena saber cómo se comparan tus datos con un estándar de referencia incluso si no esperas que tus datos se parezcan a ese estándar de referencia. (Se ha utilizado muchos otros nombres para este gráfico, incluyendo gráfico de probabilidad normal y gráfico de puntuaciones normales).

2b. En mi opinión, los diagramas de caja suelen ser sobrevalorados a menos que el diagrama de caja también muestre detalles en la caja y dentro de las líneas verticales.

2c. Los valores atípicos marcados generalmente se verán en los histogramas. Pero ten cuidado como es costumbre con la sensibilidad del histograma a la elección del ancho del intervalo. Con conjuntos de datos muy grandes, ten en cuenta que los valores atípicos pueden formar barras casi despreciables por sí solas. (A veces es útil utilizar una variante en el histograma en la que se grafica la raíz cuadrada de la frecuencia o densidad. Los valores únicos se ven mejor de esa manera).

3. Si usas reglas generales, desconfía de ellas.

3a. Una regla general muy utilizada es cualquier valor que esté a más de 1.5 RIC de distancia del cuartil más cercano. Si rastreas esto hasta su origen en J.W. Tukey. 1977. Análisis Exploratorio de Datos. Reading, MA: Addison-Wesley, verás que nunca fue una regla general para identificar valores atípicos que debas descartar. Era una regla general para identificar puntos de datos sobre los que debes pensar.

3b. Bajo reglas generales, incluyo todas las pruebas de significancia con esta característica: supongamos que los datos deben provenir de alguna distribución nombrada. ¿Qué tan probable es que el o los valores atípicos propuestos estén en este escenario? Aquí, la trampa es que a menos que tengas motivos realmente buenos para la suposición, la lógica está en algún lugar entre dudosa y absurda. Es muy fácil elegir la distribución de chimpancés como referencia cuando tus datos son más parecidos a una distribución de gorilas. (Esto no contradice el punto 2a anterior. Un gráfico normal de cuantiles es informativo cuando la mayoría de los datos no son normales. Una prueba de significancia basada en la normalidad generalmente no lo es).

4. Considera trabajar en una escala transformada. A menudo la respuesta no es eliminar los valores atípicos, sino darte cuenta de que sería mejor trabajar con una versión transformada de una variable en la que los valores atípicos parezcan estar en línea con el resto de los datos. El ejemplo más común (pero no el único) es tomar logaritmos.

5. (Más avanzado.) Utiliza simulaciones. Si tienes una o más distribuciones nombradas particulares en mente, obtén muestras simuladas del mismo tamaño y idealmente ubicación, escala y forma similar que tus datos y observa qué tan comunes son los valores atípicos con esos datos.

6. Desarrolla precaución estadística al descartar o incluso identificar valores atípicos. Reconocer los valores atípicos es como conocer el amor verdadero. Si tienes dudas, no estás allí. Un valor atípico debería destacarse por ser muy diferente en varios sentidos (gráficos y numéricos) y también parecer realmente incómodo para tu análisis previsto. El consejo podría ser cambiar el análisis previsto, no desechar los datos como no deseados. Piensa también en el tamaño de la muestra: una muestra más grande llenaría muchos de los vacíos, y lo que parece extraño puede verse solo porque tienes una muestra pequeña.

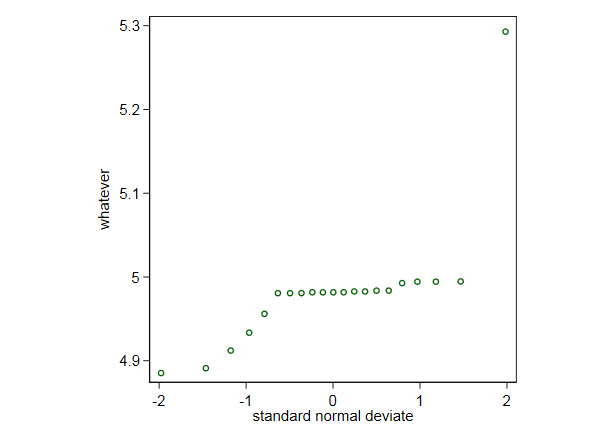
Como gesto, aquí tienes un gráfico normal de cuantiles para tus datos. El valor más alto parece desconcertante, pero ninguna cantidad de experiencia estadística puede compensar completamente no saber qué son estos datos. Al mismo tiempo, debo preguntar ¿por qué hay tantos valores muy cerca en el medio de la distribución? (No te darías cuenta de eso en un diagrama de caja).