¿Cuál es la diferencia entre la dependencia espacial y la heterogeneidad espacial?
Mi pregunta está motivada por lecturas sobre problemas de especificación de modelos en econometría espacial, en particular Anselin (2010).
Estos términos probablemente no tienen una definición técnica universalmente aceptada, pero sus significados son razonablemente claros: se refieren a la variación de segundo y primer orden de un proceso espacial, respectivamente. Veámoslos en orden después de introducir algunos conceptos estándar.
Un proceso espacial o proceso estocástico espacial puede ser pensado como una colección de variables aleatorias indexadas por puntos en un espacio. (Las variables tienen que cumplir algunas condiciones técnicas naturales para calificar como un proceso: ver el Teorema de Extensión de Kolmogorov).
Es importante señalar que un proceso espacial es un modelo. Es válido utilizar múltiples modelos diferentes (conflictivos) para analizar y describir los mismos datos. Por ejemplo, los modelos de concentraciones naturales de metales en suelos pueden ser puramente estocásticos para regiones pequeñas (como una hectárea o menos), mientras que sobre regiones extensas (que abarcan varios kilómetros) es usualmente importante describir tendencias regionales subyacentes de manera determinista, es decir, como una forma de heterogeneidad espacial.
Heterogeneidad espacial es una propiedad de un proceso espacial cuya media (o "intensidad") varía de punto a punto.
La media es una propiedad de primer orden de una variable aleatoria (relacionada con su primer momento), por lo tanto la heterogeneidad espacial puede ser considerada una propiedad de primer orden de un proceso.
Dependencia espacial es una propiedad de un proceso estocástico espacial en el que los resultados en diferentes ubicaciones pueden estar relacionados.
Frecuentemente podemos medir la dependencia en términos de la covarianza (segundo momento) o la correlación de las variables aleatorias: en este sentido, la dependencia puede ser pensada como una propiedad de segundo orden. (Los puristas rápidamente señalarán que correlación e independencia no son lo mismo, por lo que equiparar dependencia con propiedades de segundo orden, aunque intuitivamente útil, no es generalmente válido).
Cuando se observan patrones en datos espaciales, generalmente se pueden describir como heterogeneidad o dependencia (o ambas), dependiendo del propósito del análisis, la información previa y la cantidad de datos.
Algunos ejemplos simples y bien estudiados ilustran estas ideas.
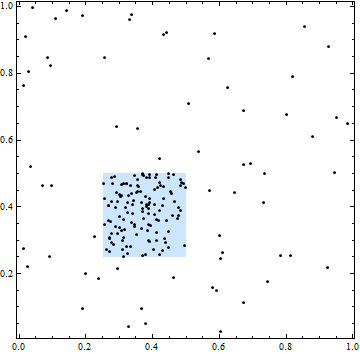
En esta figura, el cuadrado delimita un área de mayor intensidad espacial. Sin embargo, todas las ubicaciones de puntos son independientes: el agrupamiento y los huecos en los puntos son típicos de ubicaciones independientemente seleccionadas al azar.
La dependencia espacial en este proceso gaussiano es evidente a través de los patrones de crestas y valles. Sin embargo, son homogéneos: no hay una tendencia general. Sin embargo, si nos enfocáramos en una pequeña parte de esta área, podríamos optar por tratarlo como un proceso no homogéneo (es decir, con una tendencia) en su lugar. Esto ilustra cómo la escala puede influenciar en el modelo que elegimos.
Esta imagen muestra una realización diferente del componente aleatorio de este proceso de la utilizada en la ilustración anterior, por lo que los patrones de pequeñas ondulaciones no serán exactamente iguales que antes, pero tendrán las mismas propiedades estadísticas.
Respuesta increíble, de hecho. Una pequeña pregunta/comentario adicional: si existe una tendencia en los datos (heterogeneidad espacial) entonces hay áreas donde las observaciones cercanas son similares/tienen la misma media. ¿No se sigue que estas observaciones son dependientes espacialmente, al menos en un sentido informal?
@Julian Sí, eso es correcto. Por eso la forma subyacente del proceso no se puede identificar de manera única solo examinando los datos. Para más discusión, consulta mi respuesta en stats.stackexchange.com/a/35524, donde tu conclusión está respaldada con un cálculo formal.
La noción de heterogeneidad espacial en las estadísticas espaciales actuales solo se utiliza para caracterizar la varianza local de la dependencia espacial o regresión. Sugiero una perspectiva amplia sobre la heterogeneidad espacial, que se refiere al patrón de escalado de muchas más cosas pequeñas que grandes. Es importante destacar que el patrón de escalado se repite múltiples veces, medido por el índice ht.
Bajo la nueva definición, la heterogeneidad espacial debe formularse como una ley de escala. Por lo tanto, la heterogeneidad es similar a una ley de potencia en lugar de una distribución gaussiana.
Con esta perspectiva amplia, tanto la dependencia espacial como la heterogeneidad describen la verdadera imagen de la superficie terrestre. Hay muchas más cosas pequeñas que grandes en todas las escalas o globalmente, pero las cosas son más o menos similares en una escala o localmente; consulte este documento para más detalles.
https://www.researchgate.net/publication/282310447_A_Fractal_Perspective_on_Scale_in_Geography
Creo que esta publicación se beneficiaría de hacer una comparación más explícita (particularmente señalando cualquier distinción) entre la heterogeneidad y la dependencia. La pregunta fue qué diferencia hay entre las dos. Puedo ver que "tanto la dependencia espacial como la heterogeneidad representan una imagen real de la superficie terrestre" señala una similitud entre los conceptos, pero ¿cuál es la distinción entre ellos? ¿Representan esta imagen de diferentes maneras?
Hay una gran diferencia entre los dos bajo la nueva definición de heterogeneidad, sin embargo, hay poca diferencia entre los dos bajo la antigua definición de heterogeneidad. Bajo la antigua definición, la heterogeneidad espacial se refiere a cómo la dependencia espacial o la regresión varía de un lugar local a otro. Bajo la nueva definición de heterogeneidad (que es esencialmente la misma definición que en otras ciencias como la biología y la física), la heterogeneidad espacial se formula como una ley de escalamiento que es universal y general. Creo que la distinción no es solo técnica, sino a nivel de paradigma.
Gracias. Creo que la respuesta se beneficiaría incluyendo parte de esa discusión (hay un botón de edición en la parte inferior de la respuesta). Aprecio que esto pueda estar tratado en los artículos vinculados, pero nos gusta que nuestras respuestas sean autocontenidas en lugar de depender de enlaces externos.
La pregunta depende de la definición matemática de los dos conceptos. Ya existen varias definiciones de autocorrelación espacial como el Índice de Moran, pero pocas de heterogeneidad espacial, probablemente porque esta última depende de la escala y sería diferente en escalas distintas. Definí la heterogeneidad espacial estratificada (se espera que el artículo completo esté en línea el 12 de marzo de 2016 en la revista Ecological Indicators):
Una medida de heterogeneidad espacial estratificada
Jin-Feng Wang1*, Tong-Lin Zhang2, Bo-Jie Fu3
RESUMEN
La heterogeneidad espacial estratificada, que se refiere a la varianza dentro de las estratas menor que la varianza entre estratas, es ubicua en fenómenos ecológicos, como zonas ecológicas y muchas variables ecológicas. La heterogeneidad espacial estratificada refleja la esencia de la naturaleza, implica posibles mecanismos distintos por estratas, sugiere posibles determinantes del proceso observado, permite la representatividad de las observaciones de la tierra, y refuerza la aplicabilidad de inferencias estadísticas. En este documento, proponemos un método de estadística q para medir el grado de heterogeneidad espacial estratificada y para probar su significancia. El valor de q está entre [0, 1] (0 si una estratificación espacial de la heterogeneidad no es significativa, y 1 si hay una estratificación espacial perfecta de la heterogeneidad). Se deriva la función de densidad de probabilidad exacta. El estadístico q se ilustra con dos ejemplos, en los que evaluamos las heterogeneidades espaciales estratificadas de un mapa manual y la distribución del NDVI anual en China. --Jinfeng Wang 2016-3-8
I-Ciencias es una comunidad de estudiantes y amantes de la ciencia en la que puedes resolver tus problemas y dudas.
Puedes consultar las preguntas de otros usuarios, hacer tus propias preguntas o resolver las de los demás.
1 votos
La referencia sería útil. Desde mi experiencia personal, no todos los términos están aún fijados en la econometría espacial, es decir, diferentes autores pueden dar diferentes definiciones.
1 votos
¡Tengo la sensación de que Luc Anselin escribió más de un artículo en 2010! Una cita más específica (junto con un enlace) sería útil (aunque ha utilizado estos términos desde su libro de Econometría Espacial impreso en 1988).
0 votos
Gracias por la sugerencia - He añadido un enlace al artículo.