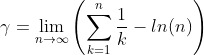La Constante de Euler se define como el límite de la diferencia de la sucesión de sumas parciales de la serie armónica y el logaritmo neperiano.
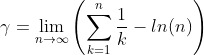
La Constante fué publicada en 1734 `por el matemático Suizo Leonard Euler en su Obra "De Progressionibus Harmonicus Observations"
La Expresión;
conocida como Suma Armónica corresponde a un número racional a/b con a y b>0 Números enteros.
Para el análisis de ln(n) con n número Racional Entero nos basaremos en los Sgtes Teoremas
Teorema de Hermite - Lindemann: Si es un número *Algebraico** distinto de 0, entonces el número
es Trascendente
Y por Contraposición Lógica del Teorema Anterior , Tenemos el Siguiente
Corolario de Teorema de Hermite - Lindemann. : Si es un número Algebraico
Entonces es Trascendente
Ahora Analizamos ln(n) con n Número Real Entero Algebraico
Tenemos;
Entonces Debemos conocer y/o Analizar las condiciones de la variable x para que
La Expresión; Sea un Número Racional Entero
Expresamos la Función Exponencial por la Fracción Continua de Euler
Aquí nos basamos en que Todo número Racional se puede expresar como Fracción Continua Finita
Tambien podemos analizar en función del Radio de Convergencia para el desarrollo de Taylor de la Función Exponencial.
Desarrollamos la función exponencial ,en Series de Potencia de (x-0) , es decir, con centro en x=0
y obtenemos la Expresión;
Luego obtenemos el Radio de Convergencia:
Simplificamos :
Obtenemos :
Donde obtenemos que R tIende a Infinito ; Es Decir , la Serie Converge para todo valor de
Sabemos que Todo Número Real puede ser Racional o Irracional,Algebraico o Trascendente , Lo importante es la condición de existencia para la convergencia Para todo x Real, Por lo tanto, tenemos que...
; Verificamos que n , Número Entero Natural, es un número Algebraico.
Por Teoría de Números Sabemos :
Donde : Conjunto de los Números Algebraicos.
Específicamente :
Es decir:
Por lo Tanto:
Es decir que n Numéro Racional Natural es Algebraico
Ahora ,.de Corolario de Teorema de Hermite - Lindemann , deducimos que
ln(n) es Trascendente y por lo Tanto Irracional.
Ya que por Teoría de Números Sabemos que:
Donde Tr = Conjunto de los números Trascendentes
e; I =Conjunto Números Irracionales
Ahora Analizamos la Naturaleza de la Constante en base a la Expresión Citada.:
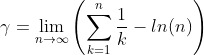
De algebra de límites tenemos:
De Teoría de Números Sabemos que : El Conjunto de los Números Naturales N es Infinito, es decir , que para valores suficientemente Grandes o inconmensurables de N , los Números Naturales ( o Componentes del Conjunto de Números Naturales) Conservan sus Propiedades.
Entonces Tenemos que : Es un Número Racional con a, b>0 Números Naturales
Y es un número irracional.
Ahora Probaremos por Contradicción que la diferencia de límites de estas expresiones, es decir , de la
expresión 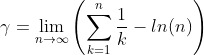Conocida como la Constante de Euler es un Número Irracional
Planteamos la expresión :
Y planteamos como Hipótesis que : es un número Racional...
Luego:
Tenemos que en el Lado Izquierdo las expresiones ad - bc y bd Corresponden a Números Enteros, ya que el producto de nuḿeros enteros es un número entero ( Similarmente con la Suma y Resta)
Por lo tanto la Expresión: corresponde a un Número Racional , lo que está en contradicción con el Lado Derecho I que corresponde a un Número Irracional, Por lo tanto ,
la Expresión: : es un Número Irracional .
Luego , La Expresión: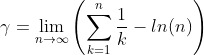
Debe Corresponder a un Número Irracional.
Gracias por Vuestra Lectura...!
Atte.. Bruno A. Savron.:
