¿Cuál es el significado físico de las ecuaciones de Navier-Stokes?

Question

¿Cuál es el significado físico de las ecuaciones de Navier-Stokes?

Estoy tratando de entender el significado físico de las ecuaciones de Navier-Stokes. Pero hasta ahora no he obtenido una respuesta razonable.

Answer 1

Estrictamente hablando, la ecuación de Navier-Stokes se usa para la ecuación vectorial (o las ecuaciones escalares en cada dirección del espacio) que describe la conservación del momento para un trozo continuo y deformable de masa, un continuo, que se caracteriza por sus propiedades viscosas (básicamente actúa como un gran amortiguador).

Más generalmente, el término se usa para el conjunto completo de ecuaciones de conservación que describen el movimiento de tal fluido (gas o líquido), es decir, la ecuación de continuidad que describe la conservación de la masa, la ecuación del momento que describe la conservación del momento similar a la segunda ley de Newton $\vec F = m \vec a$ y la ecuación de energía que describe la conservación de la energía total $e := e_{in} + \sum\limits_{j \in \mathcal{D}} \frac{u_j u_j}{2}$ ($\mathcal{D}$ aquí denota las posibles dimensiones espaciales $\{ x, y, z \}$).

---

Suposición básica: hipótesis del continuo

La hipótesis del continuo se basa en una visión macroscópica que ignora la presencia de átomos y moléculas y simplemente asume que el material de interés es tan denso que se pueden encontrar valores límite para variables macroscópicas como la densidad $\rho$ y la presión $p$. La desviación de ese estado ideal se caracteriza por el número de Knudsen $Kn$ y hace que las ecuaciones se descompongan para sustancias muy diluidas como flujos de gas rarificados que pueden ser relevantes para el reingreso de una nave espacial. No obstante, las ecuaciones se pueden aplicar a la mayoría de los casos de flujo de fluidos, incluido el flujo de agua, la aerodinámica de los automóviles, el flujo a escalas muy pequeñas (microfluídica) y el flujo supersónico alrededor de aviones de combate.

Navier-Stokes como un conjunto de ecuaciones de advección-difusión

Todas las ecuaciones de conservación toman la forma de una ecuación de advección-difusión (aquí en notación diferencial que asume la suavidad de las soluciones por lo que no se puede aplicar a discontinuidades en el flujo como choques, de esa manera una formulación integral es más general)

$$\underbrace{\frac{\partial \Phi_i}{\partial t}}_{\text{cambio temporal}} + \underbrace{\sum\limits_{j \in \mathcal{D}} \frac{\partial (\Phi_i u_j )}{\partial x_j }}_{\text{cambio debido a la advección}} = \underbrace{ \sum\limits_{j \in \mathcal{D}} \frac{\partial D_i}{\partial x_j } }_{\text{difusión}} + \underbrace{S_i}_{\text{fuente}}$$

donde $\Phi_i$ es la propiedad de interés y $D_i$ un cierto flujo difusivo que suaviza la propiedad en el espacio:

$$ \vec \Phi = \left( \begin{array}{c} \rho \\ \rho u_x \\ \rho u_y \\ \rho u_z \\ \rho e \\ \end{array} \right) \hspace{2cm} \vec D = \left( \begin{array}{c} 0 \\ \sigma_{xj} \\ \sigma_{yj} \\ \sigma_{zj} \\ - q_j + \sum\limits_{i \in \mathcal{D}} u_i \sigma_{ij} \\ \end{array} \right) \hspace{2cm} \vec S = \left( \begin{array}{c} 0 \\ \rho g_x \\ \rho g_y \\ \rho g_z \\ \sum\limits_{i \in \mathcal{D}} \rho u_i g_i \\ \end{array} \right)$$

$\sigma_{ij}$ es el tensor de esfuerzos compuesto por la presión $p$ y los esfuerzos viscosos $\tau_{ij}$

$$ \sigma_{ij} := - p \delta_{ij} + \tau_{ij} $$

y $q_j$ es el flujo de calor.

Generalmente se asume que la ley del material que conecta la deformación de un elemento fluido y los esfuerzos está dado por un fluido newtoniano isotrópico y la hipótesis de Stokes

$$\tau_{ij} = 2 \mu S_{ij} - \frac{2}{3} \mu \sum\limits_{k \in \mathcal{D}} S_{kk} \delta_{ij}, $$

donde $S_{ij}$ es el tensor de velocidad de deformación

$$S_{ij} := \frac{1}{2} \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right),$$

y el flujo de calor se modela de acuerdo con la ley de Fourier

$$q_i = - k \frac{\partial T}{\partial x_i}.$$

Answer 2

En pocas palabras, las ecuaciones de Navier-Stokes son una versión continua de la segunda ley de Newton. Mantienen un registro de cómo cambia en el tiempo el momento (densidad) del fluido.

Answer 3

Es solo una ecuación de movimiento para un fluido relacionada con la segunda Ley de Newton del Movimiento. Empecemos,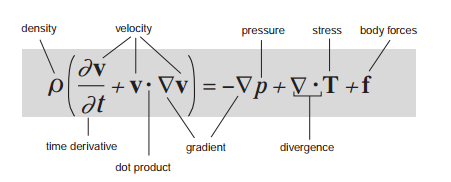

Esta es la Expresión general que se puede determinar como que, el lado izquierdo es la aceleración de una pequeña región de fluido y el lado derecho son las fuerzas que actúan sobre ella, es decir, la presión, el estrés y las fuerzas internas del cuerpo. También sigue la ley de conservación del momento. Estas ecuaciones se utilizan para resolver flujos incompresibles o compresibles, a baja o alta velocidad, fluidos no viscosos o viscosos.

Hablemos de sus ecuaciones diferenciales que describen el flujo de líquidos.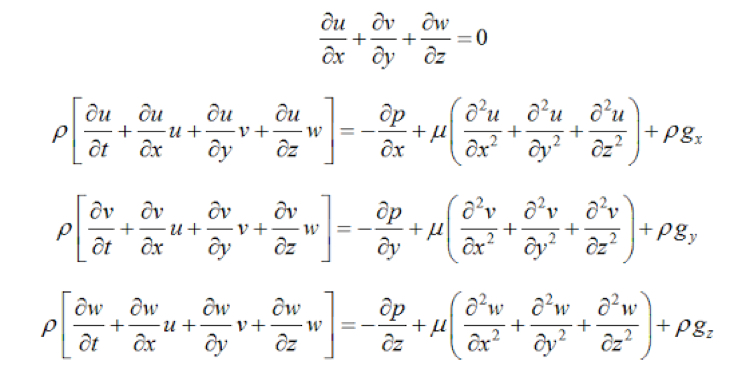

El símbolo "parcial" se usa para indicar derivadas parciales. El símbolo indica que debemos mantener todas las variables independientes fijas, excepto la variable junto al símbolo, al calcular una derivada. Los términos en el lado izquierdo de las ecuaciones de momento se llaman términos de convección de las ecuaciones. La convección es un proceso físico que ocurre en un flujo de gas en el que alguna propiedad es transportada por el movimiento ordenado del flujo. Los términos en el lado derecho de las ecuaciones de momento que se multiplican por el inverso del número de Reynolds se llaman términos de difusión. La difusión es un proceso físico que ocurre en un flujo de gas en el que alguna propiedad es transportada por el movimiento aleatorio de las moléculas del gas. La turbulencia, las capas límite, el estrés, todo esto que estudiamos en la Dinámica de Fluidos Computacional (CFD) entran en la Difusión.

Nota: En realidad son simplificaciones de las ecuaciones de Euler de la dinámica de fluidos. Las ecuaciones de Euler no tienen en cuenta los efectos de la viscosidad del fluido que sí se incluyen en las ecuaciones de Navier-Stokes.