¿Saldrá la pelota del pozo o no?

Question

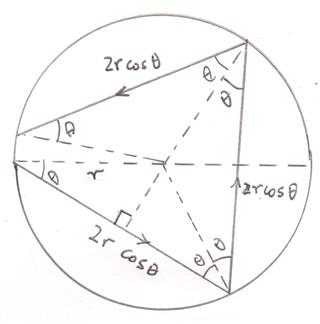
Una pequeña bola se mueve a una velocidad constante $v$ a lo largo de una superficie horizontal y en el punto $A$ cae en un pozo vertical de profundidad $H$ y radio $r$. La velocidad de la bola forma un ángulo $\theta$ con el diámetro del pozo trazado a través del punto $A$. Determine la relación entre $v, H, r, \theta$ para que la bola pueda "salir" del pozo después de impactos elásticos con las paredes (se deben descuidar las pérdidas por fricción)

La respuesta es $\dfrac{nr\cos\theta}{v}=k\sqrt{\frac{2H}{g}}$, donde $n, k$ son números enteros y primos entre sí

Mi pregunta es:

Dado que las colisiones son elásticas, la velocidad al caer debería conservarse y ayudar a la bola a salir, e incluso no hay fuerza que cambie la velocidad en la dirección horizontal, por lo que la bola debería salir del pozo/zanja sin ninguna condición matemática, pero esto no sucede en mi libro: se da una condición particular.

Quiero que PSE me diga por qué hay una condición particular para que la bola salga. ¿Por qué la bola no puede salir si se lanza a cualquier ángulo, a cualquier velocidad en el pozo?

EDITAR

Obtuve una respuesta excelente de ustedes, pero aún quiero preguntar:

¿Por qué necesitamos una condición para que la bola salga del pozo? El componente vertical de la velocidad después de que la bola golpea el suelo del pozo se convierte y eso hará que la bola suba, y no veo ningún tipo de fuerza que detenga la bola para salir del pozo.

Answer 1

Mirando desde arriba, puedes ver la simetría de la situación con la pelota golpeando una pared en un intervalo de tiempo de $\dfrac {2 r \cos \theta}{v}$ y para el movimiento vertical la pelota alcanzando nuevamente el borde en un tiempo $2 \sqrt{\dfrac {2H}{g}}$ (usando $s = \frac 1 2 g t^2$).

Entonces debes tener $\dfrac{2 n r\cos\theta}{v}=2 k \sqrt{\frac{2H}{g}}$ para que el impacto contra la pared y alcanzar la altura máxima ocurran simultáneamente donde $n$ y $k$ son enteros.

---

Luego:

Si la pelota es una masa puntual y llega justo en la parte superior de la pared, no golpeará la pared y rebotará, sino que continuará moviéndose en línea recta y escapará del pozo.

Answer 2

La única forma de que la pelota escape es si rebota varias veces y llega al borde en la parte superior de un rebote. Esta condición significa que el tiempo de vuelo horizontal debe ser una fracción racional del tiempo vertical: $t_h=\frac{m}{k}t_v$, lo que incluye todas las posibilidades, como regresar al punto inicial, salir por el otro lado, un agujero lo suficientemente grande para permitir varios rebotes horizontales, o demasiado pequeño para permitir uno antes de rebotar en la pared antes de tocar el suelo.

Answer 3

Tomemos un caso en 2D por simplicidad. Supongamos que la pelota entró en el pozo en el punto A. Golpeó en los puntos R1, H1, H2 y R2 de manera tan afortunada que encajó exactamente en el punto B y salió. Esto solo sucedió porque la proporción de diámetro a profundidad del pozo es tan buena que permitió a la pelota realizar un número finito de rebotes. Esto es posible porque el tiempo necesario para el recorrido vertical con cierto número de golpes en el fondo (digamos, Tk) es exactamente el mismo que el tiempo tomado para el otro número de golpes horizontales en la pared (Tn). En el caso desafortunado, si no puedes dividir un tiempo entre el otro y obtener un número entero, entonces la pelota entraría en un bucle infinito dentro del pozo.

Answer 4

Si la pelota es una masa puntual (sin momento angular), entonces, en una vista superior, la pelota recorrerá un patrón en forma de estrella, por ejemplo, como este (esto es para $\theta=18$ grados):

Dado que la pelota no perderá energía, continuará para siempre, aunque no necesariamente a lo largo de un patrón de estrella cerrado como en esta imagen. La pelota realiza trayectorias parabólicas, comenzando en la parte superior de una parábola. La componente horizontal de la velocidad de la pelota no cambia en magnitud, solo en dirección. Los puntos más altos de las parábolas siempre estarán exactamente a la altura del borde del pozo; se supone que la pelota escapará si ese punto más alto resulta estar en el borde, es decir, si un vértice de la estrella coincide con el punto más alto de la parábola.

Entonces: calcula la longitud $a$ de un segmento de línea individual (todos son iguales) y calcula la distancia horizontal $b$ recorrida por la pelota en una parábola completa (de punto más alto a punto más alto). La pelota saldrá si existen dos enteros $m$ y $n$ tales que $ma=nb$. Puedes averiguar por qué necesitan ser números primos entre sí.

Answer 5

Farcher proporciona una excelente explicación del problema, pero quizás no responde a tu pregunta: "¿Por qué hay algunas condiciones en las que la pelota no sale a pesar de no perder energía?" Aquí tienes un ejemplo de una de esas condiciones:

Para simplificar, digamos que $\theta\ =\ 0$ por lo que la pelota viajará directamente a través del diámetro del pozo. Imagina que la pelota cae y va lo suficientemente rápido ($v$) o que el pozo es lo suficientemente profundo ($H$) o ancho ($r$) como para que cuando la pelota golpea por primera vez el suelo del pozo casi haya alcanzado la pared opuesta al lado por el que entró. Para cuando rebota a su altura original en la parte superior del pozo, no estará justo en el borde del pozo y, por lo tanto, no podrá escapar, caerá de nuevo y continuará rebotando. Podrías imaginar que las condiciones de $v$, $H$ y $r$ son tales que se repite un ciclo para siempre, nunca en el borde del pozo cuando está en su altura máxima.