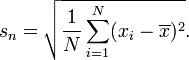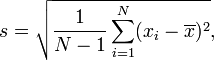Como yo entiendo las Escuelas del reino unido enseñan que la Desviación Estándar se encuentra utilizando:
mientras que NOS enseñan las Escuelas?:
(en un nivel básico de todos modos).
Esto ha causado un número de mis alumnos problemas en el pasado ya que he buscado en Internet, pero se encontró con el mal explicación.
¿Por qué la diferencia?
Con simples conjuntos de datos de decir 10 valores, ¿qué grado de error no se si el mal se aplica el método (por ejemplo, en un examen)?
La primera fórmula es la población de la desviación estándar y la segunda fórmula es la de la muestra desviación estándar. La segunda fórmula también está relacionado con el imparcial estimador de la varianza de ver wikipedia para más detalles.
Supongo (aquí) en el reino unido no hacen la distinción entre la muestra y la población, en la escuela secundaria. Ciertamente, no toque conceptos tales como estimadores sesgados.
Porque todavía nadie ha contestado a la pregunta final, es decir, para cuantificar las diferencias entre las dos fórmulas--vamos a tener cuidado de eso.
Por muchas razones, es apropiado comparar las desviaciones estándar en términos de sus coeficientes más que sus diferencias. La proporción es de
$$s_n / s = \sqrt{\frac{N-1}{N}} = \sqrt{1 - \frac{1}{N}} \approx 1 - \frac{1}{2N}.$$
La aproximación puede ser visto como el truncamiento de la (alternando) en series de Taylor para la raíz cuadrada, lo que indica que el error no puede exceder de $|\binom{1/2}{2}N^{-2}|$ = $1 / (8 N^2)$. Este establece que la aproximación es más que suficiente (para nuestros propósitos) una vez $N$ $2$ o más.
Es inmediato que las dos SD estimaciones están dentro de (sobre) 10% una vez $N$ supera $5$, dentro de los 5% una vez $N$ supera $10$, y así sucesivamente. Claramente, para muchos de los efectos de estas discrepancias son tan pequeñas que no importa qué fórmula se utiliza, especialmente cuando la tarjeta SD está destinado a describir la propagación de datos o para la fabricación de semi-cuantitativos de las evaluaciones o predicciones (como en el empleo de la 68-95-99.7 regla de oro). Las diferencias son aún más importantes cuando se comparan SDs, como cuando se comparan los diferenciales de dos conjuntos de datos. (Cuando los conjuntos de datos son equinumerous, las diferencias prácticamente desaparecen por completo, y ambas fórmulas conducir a conclusiones idénticas.) Podría decirse que estas son las formas de razonamiento que están tratando de enseñar a los estudiantes principiantes, así que si los estudiantes son cada vez preocupa que la fórmula a utilizar, que podría ser tomado como una señal de que el texto o en la clase es no dando énfasis a lo que es realmente importante.
Debemos prestar atención en el caso de muy pequeño $N$. Aquí, la gente puede ser el uso de $t$ pruebas en lugar de $z$ pruebas, por ejemplo. En ese caso, es indispensable emplear cualquiera que sea la fórmula para la desviación estándar es utilizado por uno de la tabla o de software. (Esto no es una cuestión de una fórmula bien o mal, es solo una consistencia requisito). La mayoría de las tablas de uso $s$, no $s_n$: este es el único lugar en la primaria plan de estudios donde el texto y el maestro deben ser claros acerca de que la fórmula a utilizar.
No estoy seguro de que esto es puramente un Estados Unidos frente Británico problema. Aquí está una breve página que escribí explicando la diferencia entre el uso de n vs n-1 cuando el cálculo de una Desviación Estándar.
Esta es la Corrección de Bessel. La versión estadounidense se muestra la fórmula para la desviación estándar de la muestra, donde el reino unido la versión anterior es la desviación estándar de la muestra.
Puesto que N es el número de puntos en el conjunto de datos, se podría argumentar que por el cálculo de la media que uno ha reducido el grado de libertad en el conjunto de datos por uno (ya que presenta una dependencia en el conjunto de datos), así que uno debe usar N-1 a la hora de estimar la desviación estándar de un conjunto de datos para que uno tenía para estimar la media antes.
I-Ciencias es una comunidad de estudiantes y amantes de la ciencia en la que puedes resolver tus problemas y dudas.
Puedes consultar las preguntas de otros usuarios, hacer tus propias preguntas o resolver las de los demás.
