Teorema del límite central para medianas de muestra

Question

Si calculo la mediana de un número suficientemente grande de observaciones extraídas de la misma distribución, ¿indica el teorema del límite central que la distribución de las medianas aproximará a una distribución normal? Mi entendimiento es que esto es cierto con las medias de un gran número de muestras, pero ¿también es cierto con las medianas?

Si no es así, ¿cuál es la distribución subyacente de las medianas de la muestra?

Answer 1

Si trabajas en términos de variables indicadoras (es decir, $Z_i = 1$ si $X_i \leq x$ y $0$ de lo contrario), puedes aplicar directamente el teorema del límite central a una media de $Z$'s, y usando el método Delta, convertirlo en una distribución normal asintótica para $F_X^{-1}(\bar{Z})$, lo que a su vez significa que se obtiene una normalidad asintótica para cuantiles fijos de $X$.

Así que no solo la mediana, sino cuartiles, percentiles 90, ... etc.

De manera general, si hablamos del cuantil muestral $q$-ésimo en muestras suficientemente grandes, tenemos que aproximadamente tendrá una distribución normal con media el cuantil poblacional $x_q$-ésimo y varianza $q(1-q)/(nf_X(x_q)^2)$.

Por lo tanto, para la mediana ($q = 1/2$), la varianza en muestras suficientemente grandes será aproximadamente $1/(4nf_X(\tilde{\mu})^2)$.

Necesitas que todas las condiciones a lo largo del camino se cumplan, por supuesto, por lo que no funciona en todas las situaciones, pero para distribuciones continuas donde la densidad en el cuantil poblacional es positiva y diferenciable, etc, ...

Además, no funciona para cuantiles extremos, porque el TLC no se aplica allí (el promedio de Z no será asintóticamente normal). Necesitas una teoría diferente para valores extremos.

---

Edición: La crítica de whuber es correcta; esto funcionaría si $x$ fuera una mediana poblacional en lugar de una mediana muestral. El argumento debe modificarse para que funcione correctamente.

Answer 2

@EngrStudent illuminating answer tells us that we should expect resultados diferentes cuando la distribución es continua, y cuando es discreta (los gráficos "rojos", donde la distribución asintótica de la mediana de la muestra falla espectacularmente en parecer normal, corresponden a las distribuciones Binomial(3), Geométrica(11), Hipergeométrica(12), Binomial Negativa(14), Poisson(18), Uniforme Discreta(22)).

Y de hecho este es el caso. Cuando la distribución es discreta, las cosas se complican. Proporcionaré la prueba para el Caso Absolutamente Continuo, esencialmente detallando la respuesta ya dada por @Glen_b, y luego discutiré un poco qué sucede cuando la distribución es discreta, proporcionando también una referencia reciente para quienes estén interesados en profundizar.

DISTRIBUCIÓN ABSOLUTAMENTE CONTINUA
Considere una colección de variables aleatorias i.i.d. absolutamente continuas $\{X_1,...X_n\}$ con función de distribución (cdf) $F_X(x) = P(X_i\le x)$ y función de densidad $F'_X(x)=f_X(x)$. Defina $Z_i\equiv I\{X_i\le x\}$ donde $I\{\}$ es la función indicadora. Por lo tanto $Z_i$ es una v.a. Bernoulli, con $$E(Z_i) = E\left(I\{X_i\le x\}\right) = P(X_i\le x)=F_X(x),\;\; \text{Var}(Z_i) = F_X(x)[1-F_X(x)],\;\; \forall i$$

Sea $Y_n(x)$ la media muestral de estos Bernoullis i.i.d., definida para un $x$ fijo como $$Y_n(x) = \frac 1n\sum_{i=1}^nZ_i$$ lo que significa que $$E[Y_n(x)] = F_X(x),\;\; \text{Var}(Y_n(x)) = (1/n)F_X(x)[1-F_X(x)]$$ Se aplica el Teorema del Límite Central y tenemos

$$\sqrt n\Big(Y_n(x) - F_X(x)\Big) \rightarrow_d \mathbb N\left(0,F_X(x)[1-F_X(x)]\right) $$

Observar que $Y_n(x) = \hat F_n(x)$ es decir, no es más que la función de distribución empírica. Al aplicar el "Método Delta" tenemos que para una función continua y diferenciable $g(t)$ con derivada distinta de cero $g'(t)$ en el punto de interés, obtenemos

$$\sqrt n\Big(g[\hat F_n(x)] - g[F_X(x)]\Big) \rightarrow_d \mathbb N\left(0,F_X(x)[1-F_X(x)]\cdot\left(g'[F_X(x)]\right)^2\right) $$

Ahora, elija $g(t) \equiv F^{-1}_X(t),\;\; t\in (0,1)$ donde $^{-1}$ denota la función inversa. Esta es una función continua y diferenciable (ya que $F_X(x)$ lo es), y por el Teorema de la Función Inversa tenemos

$$g'(t)=\frac {d}{dt}F^{-1}_X(t) = \frac 1{f_x\left(F^{-1}_X(t)\right)}$$

Insertando estos resultados sobre $g$ en el resultado asintótico derivado del método delta tenemos

$$\sqrt n\Big(F^{-1}_X(\hat F_n(x)) - F^{-1}_X(F_X(x))\Big) \rightarrow_d \mathbb N\left(0,\frac {F_X(x)[1-F_X(x)]}{\left[f_x\left(F^{-1}_X(F_X(x))\right)\right]^2} \right) $$

y simplificando,

$$\sqrt n\Big(F^{-1}_X(\hat F_n(x)) - x\Big) \rightarrow_d \mathbb N\left(0,\frac {F_X(x)[1-F_X(x)]}{\left[f_x(x)\right]^2} \right) $$

.. para cualquier $x$ fijo. Ahora establezca $x=m$, la mediana (verdadera) de la población. Entonces tenemos $F_X(m) = 1/2$ y el resultado general anterior se convierte, para nuestro caso de interés,

$$\sqrt n\Big(F^{-1}_X(\hat F_n(m)) - m\Big) \rightarrow_d \mathbb N\left(0,\frac {1}{\left[2f_x(m)\right]^2} \right) $$

Pero $F^{-1}_X(\hat F_n(m))$ converge a la mediana de la muestra $\hat m$. Esto se debe a que

$$F^{-1}_X(\hat F_n(m)) = \inf\{x : F_X(x) \geq \hat F_n(m)\} = \inf\{x : F_X(x) \geq \frac 1n \sum_{i=1}^n I\{X_i\leq m\}\}$$

El lado derecho de la desigualdad converge a $1/2$ y el menor $x$ para el cual eventualmente $F_X \geq 1/2$, es la mediana de la muestra.

Así que obtenemos

$$\sqrt n\Big(\hat m - m\Big) \rightarrow_d \mathbb N\left(0,\frac {1}{\left[2f_x(m)\right]^2} \right) $$ que es el Teorema del Límite Central para la mediana de la muestra de distribuciones absolutamente continuas.

DISTRIBUCIONES DISCRETAS
Cuando la distribución es discreta (o cuando la muestra contiene empates) se ha argumentado que la definición "clásica" de cuantiles muestrales, y por lo tanto de la mediana también, puede ser engañosa en primer lugar, ya que el concepto teórico a utilizar para medir lo que se intenta medir por cuantiles.
En cualquier caso se ha simulado que bajo esta definición clásica (la que todos conocemos), la distribución asintótica de la mediana de la muestra no es normal y es una distribución discreta.

Una definición alternativa de cuantiles muestrales es mediante el uso del concepto de la función de "mid-distribución", que se define como $$F_{mid}(x) = P(X\le x) - \frac 12P(X=x)$$

La definición de cuantiles muestrales a través del concepto de función de mid-distribución se puede ver como una generalización que puede abarcar como casos especiales las distribuciones continuas, pero también las no tan continuas también.

Para el caso de las distribuciones discretas, entre otros resultados, se ha encontrado que la mediana de la muestra definida a través de este concepto tiene una distribución asintóticamente normal con una ...varianza de aspecto elaborado.

La mayoría de estos son resultados recientes. La referencia es Ma, Y., Genton, M. G., & Parzen, E. (2011). Propiedades asintóticas de cuantiles de muestra de distribuciones discretas. Anales del Instituto de Matemáticas Estadísticas, 63(2), 227-243., donde se puede encontrar una discusión y enlaces a la literatura relevante más antigua.

Answer 3

Sí lo es, y no solo para la mediana, sino para cualquier cuantil de muestra. Copiando de este artículo, escrito por T.S. Ferguson, un profesor de UCLA (su página es aquí), que trata interesantemente sobre la distribución conjunta de la media de muestra y los cuantiles de muestra, tenemos:

Sea $X_1, . . . ,X_n$ i.i.d. con función de distribución $F(x)$, densidad $f(x)$, media $\mu$ y varianza finita $\sigma^2$. Sea $0 < p < 1$ y sea $x_p$ el $p$-ésimo cuantil de $F$, de modo que $F(x_p) = p$. Supongamos que la densidad $f(x)$ es continua y positiva en $x_p$. Sea $Y_n = X_{(n:\lceil np\rceil)}$ el cuantil $p$-ésimo de muestra. Entonces

$$\sqrt n(Y_n - x_p) \xrightarrow{d} N(0, p(1 - p)/(f(x_p))^2)$$

Para $p=1/2 \Rightarrow x_p=m$ (mediana), y tienes el TCL para medianas,

$$\sqrt n(Y_n - m) \xrightarrow{d} N\left(0, [2f(m)]^{-2}\right)$$

Answer 4

Me gusta la respuesta analítica dada por Glen_b. Es una buena respuesta.

Necesita una imagen. Me gustan las imágenes.

Aquí hay áreas de elasticidad en una respuesta a la pregunta:

• Hay muchas distribuciones en el mundo. La eficiencia es probable que varíe.
• Suficiente tiene diferentes significados. Para un contraejemplo de una teoría, a veces se requiere un solo contraejemplo para que se cumpla "suficiente". Para demostrar tasas de defectos bajas utilizando incertidumbre binomial, pueden ser necesarios cientos o miles de muestras.

Para una normal estándar utilicé el siguiente código de MatLab:

mysamples=1000;

loops=10000;

y1=median(normrnd(0,1,mysamples,loops));

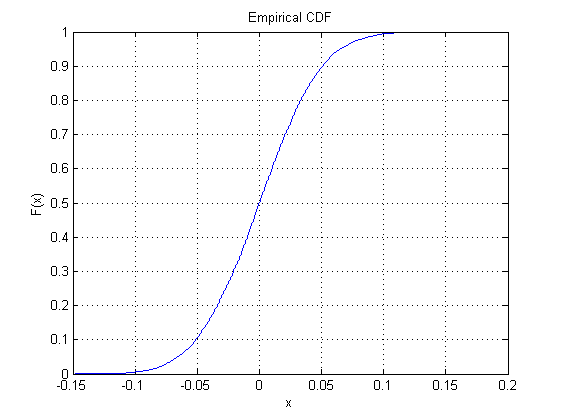
cdfplot(y1)

y obtuve el siguiente gráfico como resultado:

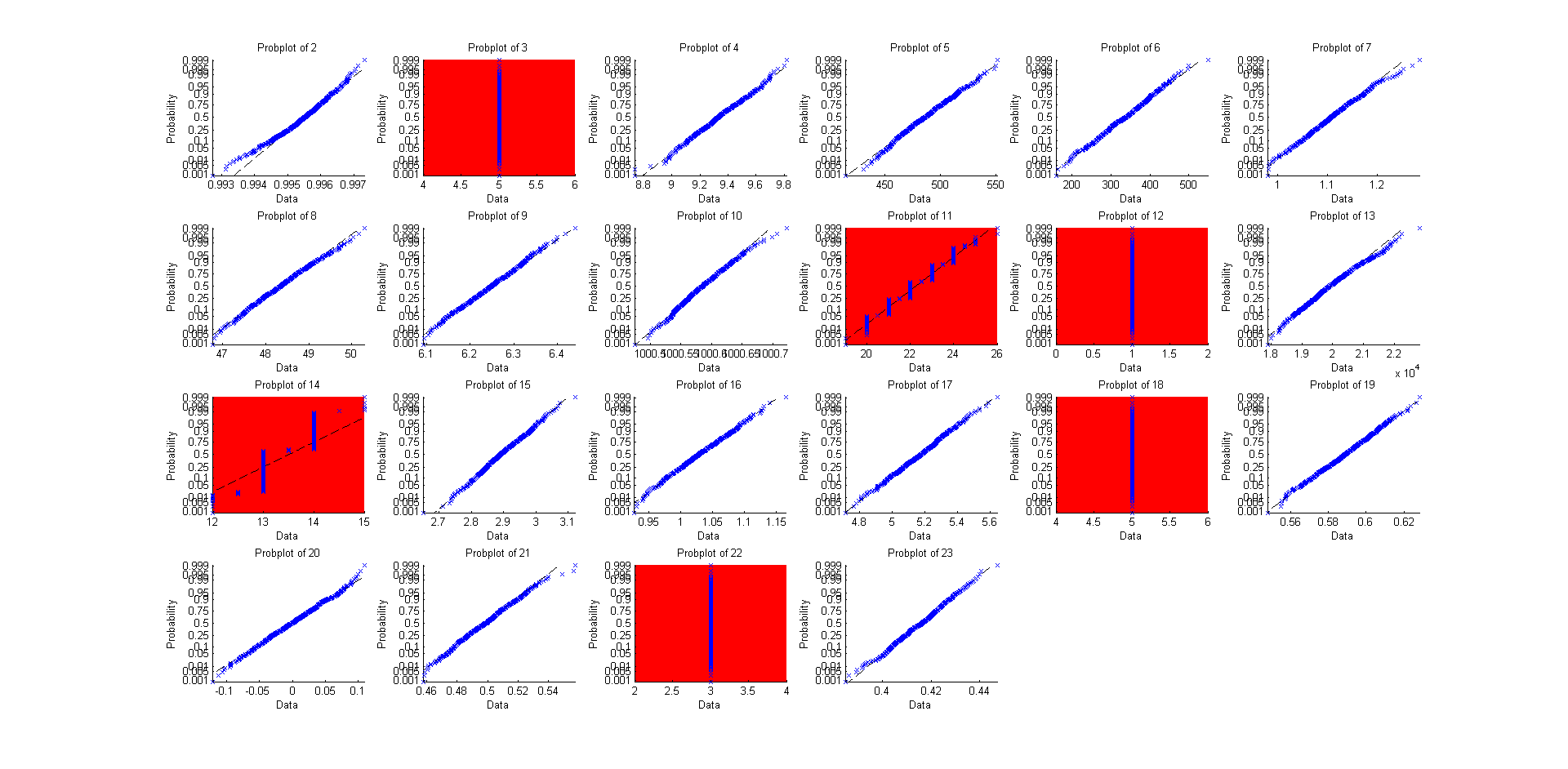
Así que, ¿por qué no hacer esto para las otras 22 o así "distribuciones integradas", excepto usando gráficos de probabilidad (donde una línea recta significa muy similar a una distribución normal)?

Y aquí está el código fuente para ello:

mysamples=1000;

loops=600;

y=zeros(loops,23);

y(:,1)=median(random('Normal', 0,1,mysamples,loops));

y(:,2)=median(random('beta', 5,0.2,mysamples,loops));
y(:,3)=median(random('bino', 10,0.5,mysamples,loops));
y(:,4)=median(random('chi2', 10,mysamples,loops));
y(:,5)=median(random('exp', 700,mysamples,loops));

y(:,6)=median(random('ev', 700,mysamples,loops));
y(:,7)=median(random('f', 5,3,mysamples,loops));
y(:,8)=median(random('gam', 10,5,mysamples,loops));
y(:,9)=median(random('gev', 0.24, 1.17, 5.8,mysamples,loops));
y(:,10)=median(random('gp', 0.12, 0.81,mysamples,loops));

y(:,11)=median(random('geo', 0.03,mysamples,loops));
y(:,12)=median(random('hyge', 1000,50,20,mysamples,loops));
y(:,13)=median(random('logn', log(20000),1.0,mysamples,loops));
y(:,14)=median(random('nbin', 2,0.11,mysamples,loops));
y(:,15)=median(random('ncf', 5,20,10,mysamples,loops));

y(:,16)=median(random('nct', 10,1,mysamples,loops));
y(:,17)=median(random('ncx2', 4,2,mysamples,loops));
y(:,18)=median(random('poiss', 5,mysamples,loops));
y(:,19)=median(random('rayl', 0.5,mysamples,loops));
y(:,20)=median(random('t', 5,mysamples,loops));

y(:,21)=median(random('unif',0,1,mysamples,loops));
y(:,22)=median(random('unid', 5,mysamples,loops));
y(:,23)=median(random('wbl', 0.5,2,mysamples,loops));

figure(1); clf
hold on

for i=2:23
    subplot(4,6,i-1)

    probplot(y(:,i))
    title(['Gráfico de probabilidad de ' num2str(i)])
    axis tight

    if not(isempty(find(i==[3,11,12,14,18,22])))
        set(gca,'Color','r')
    end

end

Cuando veo la prueba analítica, podría pensar "en teoría todos podrían encajar", pero cuando lo pruebo, entonces puedo moderar eso con "hay varias formas en las que esto no funciona tan bien, a menudo involucrando valores discretos o altamente restringidos" y esto podría hacerme querer ser más cuidadoso al aplicar la teoría a cualquier cosa que cueste dinero.

Buena suerte.