Desde la función de densidad de distribución podríamos identificar una media (=0) para la distribución de Cauchy tal como muestra el gráfico a continuación. ¿Pero por qué decimos que la distribución de Cauchy no tiene media?
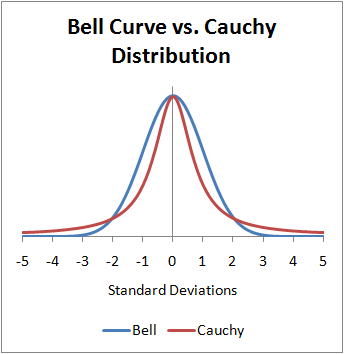
Desde la función de densidad de distribución podríamos identificar una media (=0) para la distribución de Cauchy tal como muestra el gráfico a continuación. ¿Pero por qué decimos que la distribución de Cauchy no tiene media?

Puede comprobar mecánicamente que el valor esperado no existe, pero esto debería ser intuitivo físicamente, al menos si acepta el principio de Huygens y la Ley de los Grandes Números. La conclusión de la Ley de los Grandes Números falla para una distribución de Cauchy, por lo que no puede tener una media. Si promedia $n$ variables aleatorias de Cauchy independientes, el resultado no converge a $0$ cuando $n\to \infty$ con probabilidad $1$. Permanece una distribución de Cauchy del mismo tamaño. Esto es importante en óptica.
La distribución de Cauchy es la intensidad normalizada de la luz en una línea desde una fuente de punto. El principio de Huygens dice que puede determinar la intensidad asumiendo que la luz es reemitida desde cualquier línea entre la fuente y el objetivo. Por lo tanto, la intensidad de la luz en una línea a $2$ metros de distancia se puede determinar asumiendo que la luz primero golpea una línea a $1$ metro de distancia y es reemitida en cualquier ángulo hacia adelante. La intensidad de la luz en una línea a $n$ metros de distancia se puede expresar como la convolución $n$-fold de la distribución de luz en una línea a $1$ metro de distancia. Es decir, la suma de $n$ distribuciones independientes de Cauchy es una distribución de Cauchy escalada por un factor de $n.
Si la distribución de Cauchy tuviera una media, entonces el percentil $25$ de la convolución $n$-fold dividido por $n$ debería converger a $0$ por la Ley de los Grandes Números. En cambio, permanece constante. Si marca el percentil $25$ en una línea (transparente) a $1$ metro de distancia, $2$ metros de distancia, etc. entonces estos puntos forman una línea recta, a $45$ grados. No se doblan hacia $0.
Esto te informa sobre la distribución de Cauchy en particular, pero deberías conocer la prueba integral porque hay otras distribuciones sin media que no tienen una clara interpretación física.
+1 Ahora hay una respuesta iluminadora :-) (disculpa). Por cierto, el principio lleva el nombre de Christiaan Huygens, no Huygen. Huygens fue el primero en apreciar nuevos desarrollos en probabilidad publicados en la década de 1650 por Pascal (basados en sus cartas con Fermat): fue el relato de Huygens sobre estas ideas (1657), incluida la de expectativa, lo que originalmente puso la teoría de probabilidad en un terreno matemático y allanó el camino para el seminal tratado (póstumo) de Jakob Bernoulli (Ars Conjectandi, 1713).
Esta es una respuesta excelente, pero encuentro el final confuso: "...marcar el percentil 25 en... una línea recta, a 45 grados. No se doblan hacia 0". La afirmación en sí es cierta (como consecuencia del principio de Huygens-Fresnel), pero eso es antes de "dividido por $n$". Cuando se divide por 2 a 2 metros, dividido por 3 a 3 metros, ..., entonces la línea transparente es vertical (perpendicular a la pantalla que captura la luz). La línea del percentil de 45 grados pertenece a la suma de Cauchy y no ayuda con el argumento (aún).
Respuesta agregada en respuesta al comentario de @whuber en la respuesta de Michael Chernicks (Y reescrito por completo para eliminar el error señalado por whuber.)
Se dice que el valor de la integral para el valor esperado de una variable aleatoria de Cauchy está indefinido porque el valor puede ser "hecho" para ser cualquier cosa que se desee. La integral $$\int_{-\infty}^{\infty} \frac{x}{\pi(1+x^2)}\,\mathrm dx$$ (interpretada en el sentido de una integral de Riemann) es lo que comúnmente se llama una integral impropia y su valor debe ser calculado como un valor límite: $$\int_{-\infty}^{\infty} \frac{x}{\pi(1+x^2)}\,\mathrm dx = \lim_{T_1\to-\infty}\lim_{T_2\to+\infty} \int_{T_1}^{T_2} \frac{x}{\pi(1+x^2)}\,\mathrm dx$$ o $$\int_{-\infty}^{\infty} \frac{x}{\pi(1+x^2)}\,\mathrm dx = \lim_{T_2\to+\infty}\lim_{T_1\to-\infty} \int_{T_1}^{T_2} \frac{x}{\pi(1+x^2)}\,\mathrm dx$$ y por supuesto, ambas evaluaciones deberían dar el mismo valor finito. De lo contrario, se dice que la integral está indefinida. Esto muestra inmediatamente por qué la media de la variable aleatoria de Cauchy se dice que es indefinida: el valor límite en el límite interno diverge.
El valor principal de Cauchy se obtiene como un único límite: $$\lim_{T\to\infty} \int_{-T}^{T} \frac{x}{\pi(1+x^2)}\,\mathrm dx$$ en lugar de la doble limitación anterior. El valor principal de la integral de esperanza es fácilmente visto como $0$ ya que el límite tiene valor $0$ para todos los $T$. Pero esto no puede usarse para decir que la media de una variable aleatoria de Cauchy es $0$. Es decir, la media se define como el valor de la integral en el sentido habitual y no en el sentido del valor principal.
Para $\alpha > 0$, considera en su lugar la integral $$\begin{align} \int_{-T}^{\alpha T} \frac{x}{\pi(1+x^2)}\,\mathrm dx &= \int_{-T}^{T} \frac{x}{\pi(1+x^2)}\,\mathrm dx + \int_{T}^{\alpha T} \frac{x}{\pi(1+x^2)}\,\mathrm dx\\ &= 0 + \left.\frac{\ln(1+x^2)}{2\pi}\right|_T^{\alpha T}\\ &= \frac{1}{2\pi}\ln\left(\frac{1+\alpha^2T^2}{1+T^2}\right)\\ &= \frac{1}{2\pi}\ln\left(\frac{\alpha^2+T^{-2}}{1+T^{-2}}\right) \end{align}$$ que se acerca a un valor límite de $\displaystyle \frac{\ln(\alpha)}{\pi}$ cuando $T\to\infty$. Cuando $\alpha = 1$, obtenemos el valor principal $0$ discutido anteriormente. Por lo tanto, no podemos asignar un significado inequívoco a la expresión
$$\int_{-\infty}^{\infty} \frac{x}{\pi(1+x^2)}\,\mathrm dx$$ sin especificar cómo se acercaron los dos infinitos, y ignorar este punto conduce a todo tipo de complicaciones resultados incorrectos porque las cosas no siempre son lo que parecen cuando la esencia del valor principal se disfraza como la crema del valor. Esto es por qué se dice que la media de la de Cauchy variable aleatoria se dice que es indefinida en lugar de tener valor $0$, el valor principal de la integral.
Si uno está usando el enfoque de teoría de la medida para probabilidad y la integral de valor esperado es definida en el sentido de una integral de Lebesgue, entonces el problema es más simple. $\int g$ existe solo cuando $\int |g|$ es finito, y por lo tanto $E[X]$ es indefinido para una variable aleatoria de Cauchy $X$ ya que $E[|X|]$ no es finito.
La evaluación de la integral en medio es incorrecta: es cero, no un logaritmo. El problema realmente radica en evaluar los dos límites implícitos en las integrales infinitas.
@whuber Gracias por señalar el error. He reescrito completamente mi respuesta y tu comentario ya no aplica.
No entiendo por qué la expectativa de la ratio no existe. Si $ X $ e $ Y $ están distribuidos conjuntamente de forma normal con media diferente de cero, entonces la media de $ Z = \frac{X}{Y} $ está dada por $ \int \int \frac{x}{y} p \left( x, y \right) dx dy $, ¿qué me falta?
Mientras que las respuestas anteriores son explicaciones válidas de por qué la distribución de Cauchy no tiene una esperanza, encuentro que el hecho de que la razón $X_1/X_2$ de dos variables normales $\mathcal{N}(0,1)$ independientes sea Cauchy es igualmente esclarecedor: de hecho, tenemos $$ \mathbb{E}\left[ \frac{|X_1|}{|X_2|} \right] = \mathbb{E}\left[ |X_1| \right] \times \mathbb{E}\left[ \frac{1}{|X_2|} \right] $$ y la segunda esperanza es $+\infty$.
¿Es $\left|\frac{X_1}{X_2}\right|$ una variable aleatoria de Cauchy 'plizada' cuando sé que $\frac{X_1}{X_2}$ es una Cauchy estándar? ¿Cómo se puede encontrar la distribución de $\left|\frac{X_1}{X_2}\right|$?
Sí, este es el valor absoluto de una variable de Cauchy, que tiene por lo tanto la densidad $f(x)+f(-x)$ sobre los números reales positivos.
La distribución de Cauchy no tiene media porque el punto que se selecciona (0) no es una media. Es una mediana y una moda. La media para una distribución absolutamente continua se define como $\int x f(x) dx$ donde $f$ es la función de densidad y la integral se toma sobre el dominio de $f$ (que es de $-\infty$ a $\infty$ en el caso de la distribución de Cauchy). Para la densidad de Cauchy, esta integral simplemente no es finita (la mitad de $-\infty$ a $0$ es $-\infty$ y la mitad de $0$ a $\infty$ es $\infty$).
¿Podrías explicar por qué la integral $\int_{-\infty}^{\infty} x f(x)\,dx$ es "simplemente infinita" como afirmas? La mayoría de la gente diría que la integral está indefinida ya que resulta ser de la forma $\infty - \infty.
Eso es verdad, @Dilip. Además, la integral tiene un valor principal bien definido: ¡y es igual a cero! :-)
La distribución de Cauchy se piensa mejor como la distribución uniforme en un círculo unitario, por lo que sería sorprendente si el promedio tuviera sentido. Supongamos que $f$ fuera algún tipo de "función de promediado". Es decir, supongamos que, para cada subconjunto finito $X$ del círculo unitario, $f(X)$ era un punto del círculo unitario. Claramente, $f$ tiene que ser "innatural". Más precisamente, $f$ no puede ser equivariante con respecto a las rotaciones. Para obtener la distribución de Cauchy en su forma más habitual, pero menos reveladora, proyecte el círculo unitario sobre el eje x desde (0,1), y use esta proyección para transferir la distribución uniforme en el círculo al eje x.
Para entender por qué la media no existe, piense en x como una función en el círculo unitario. Es bastante fácil encontrar un número infinito de arcos disjuntos en el círculo unitario, de manera que, si uno de los arcos tiene longitud d, entonces x > 1/4d en ese arco. Por lo tanto, cada uno de estos arcos disjuntos contribuye más de 1/4 a la media, y la contribución total de estos arcos es infinita. Podemos hacer lo mismo nuevamente, pero con x < -1/4d, con una contribución total menos infinito. Estos intervalos podrían mostrarse con un diagrama, ¿pero se pueden hacer diagramas para Cross Validated?
Bienvenido al sitio, @DavidEpstein. Puedes hacer imágenes con tu software preferido y subirlas a tu respuesta haciendo clic en el pequeño icono de imagen (para iniciar el asistente) encima del campo de respuesta. Desafortunadamente, necesitas tener al menos >=10 reputación para hacerlo. Estoy seguro de que pronto la tendrás; mientras tanto, si puedes publicar la imagen en cualquier otro lugar en internet y poner un enlace a ella en tu respuesta, un usuario con mayor reputación puede obtenerla y publicarla por ti.
No estaba al tanto de que Cauchy se interpretara como una uniforme en un círculo, pero ciertamente tiene sentido. Un argumento topológico muestra que no puede haber una función continua en un círculo que tenga las propiedades de una función de promediación.
@DavidEpstein También he leído tu respuesta en la otra publicación. La proyección estereográfica es realmente interesante. En comparación, ¿puedes comentar por qué la proyección radial igualmente válida de un semicírculo no implica que la media esté bien definida? Es decir, $U \sim \mathrm{Unif}[0,1]$, luego $X \equiv \tan\left( \pi( U - \frac12 ) \right)$ es una Cauchy estándar. Geométricamente, este es el hecho básico de que un ángulo inscrito siempre es la mitad de su ángulo central correspondiente.
I-Ciencias es una comunidad de estudiantes y amantes de la ciencia en la que puedes resolver tus problemas y dudas.
Puedes consultar las preguntas de otros usuarios, hacer tus propias preguntas o resolver las de los demás.
2 votos
Recomiendo la referencia Cabeza G., U. A.. (2013). La Media de la Distribución de Cauchy. En el blog Apoyo en Matemáticas acerca de la media de la distribución de Cauchy.
1 votos
Ver mi respuesta aquí: stats.stackexchange.com/questions/94402/…