¿Por qué las líneas de curvatura principal se intersecan en la esfera?

Question

He estado observando las líneas de curvatura principal de muchas superficies y me di cuenta de que las líneas de curvatura principal de la esfera se intersecan 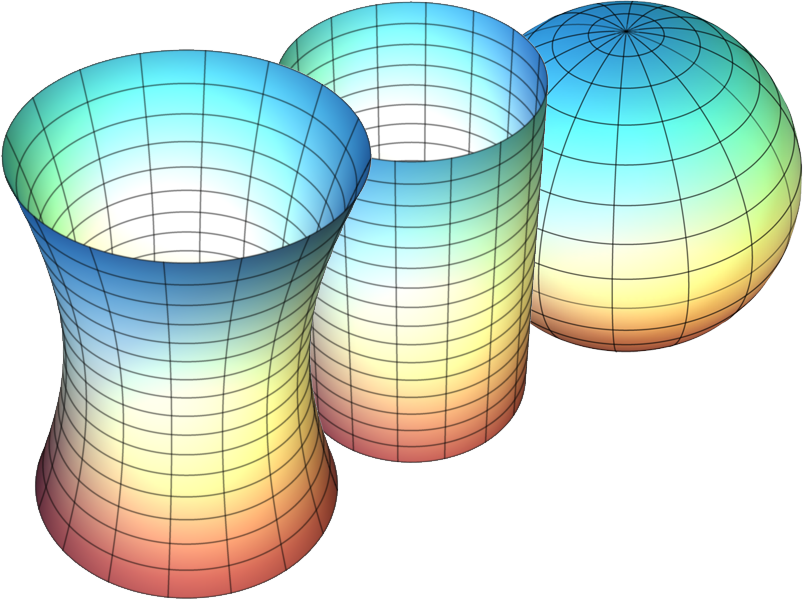, mientras que las líneas de curvatura principal de otras superficies no lo hacen.

Además, este no es el caso para todas las superficies cerradas, por ejemplo, las líneas de curvatura principal del toro de un agujero no se intersecan. Sin embargo, estas líneas para el toro de dos agujeros sí lo hacen.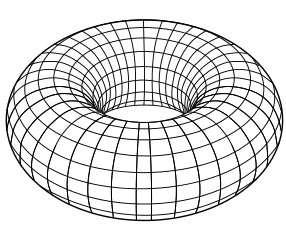

También me he estado preguntando si esto tiene alguna relación con la parametrización global o local de estas superficies, por ejemplo, hay un "tipo" diferente de discontinuidad en la parametrización de la esfera en los polos.

Answer 1

Ten cuidado: en la esfera, cualquier curva es una línea de curvatura. El fenómeno que estás notando en el toro con dos agujeros es que estas intersecciones solo pueden ocurrir en puntos umbílicos. De lo contrario, hay precisamente dos direcciones principales en cada punto y no puede haber tales intersecciones. Por supuesto, cada punto en la esfera es un punto umbílico y puedes obtener tantas intersecciones como desees tomando curvas locas (que serán líneas de curvatura). (La imagen particular que estás dibujando con Mathematica se basa en la parametrización de coordenadas esféricas, por lo que solo se refleja la singularidad del sistema de coordenadas en esta imagen.)

Answer 2

Este es un ejemplo del teorema de la bola peluda. Observa que las líneas de longitud producen un campo vectorial tangente continuo en la superficie, lo cual necesariamente tiene al menos una singularidad. De la misma manera, las líneas de latitud. (Las singularidades se encuentran en los polos en ambos casos.)

En general, esto está relacionado con la característica de Euler de la superficie. Los dos cilindros, el toro (con un agujero) y el plano tienen característica de Euler cero, por lo que no necesitan tener una singularidad. El toro con dos agujeros que dibujaste tiene característica de Euler distinta de cero, por lo que necesariamente tiene al menos una singularidad en sus campos vectoriales tangentes.

Respecto al "tipo" de singularidad, con tus curvas, la latitud de cada polo es inequívoca, pero la longitud es degenerada (similar a, en coordenadas polares, la falta de una coordenada angular definida para los puntos en el origen del sistema de coordenadas). El tipo de singularidad aquí es que al menos una curva de un conjunto de curvas es aplastada a un único punto. (En la página citada, esta es la curva/las curvas correspondientes a $f(p) =0 $, los vectores tangentes en esa curva se proyectan sobre la esfera dando vectores nulos, por lo que la curva yace en un único punto.)

Answer 3

Tenemos la relación de Euler en puntos regulares para curvas de diferenciabilidad continua $$ k_n=k_1 \cos^2\psi+ k_2\sin^2\psi $$

En puntos umbilicales, las líneas de curvatura (principales) pueden orientarse en cualquier dirección debido a la singularidad. Todos los puntos de una superficie esférica son umbilicales. Euler $k_n$ es una constante porque $k_1=k_2$.

Dos direcciones principales no pueden ser definidas en tales puntos en el eje de simetría que intersecta una superficie de revolución.