Como sabemos que una imagen virtual siempre está erguida, ¿por qué vemos una imagen virtual invertida en el lado cóncavo de una cuchara?
Por favor, ¿podrías elaborar en la última parte??
Respuestas
¿Demasiados anuncios?El problema es que la imagen que se obtiene de un espejo cóncavo es una imagen real, y no virtual.
Para entender por qué la imagen real que proviene del reflejo en una cuchara está invertida, hay que considerar el caso ideal de un espejo cóncavo, en particular (por simplicidad) uno esférico.
Suponga que el objeto que está observando, por ejemplo usted mismo, es la gran flecha verde. Puede dibujar tres rayos diferentes que parten de la punta de la flecha:
- El rayo que pasa a través del centro $C$ del espejo;
- El rayo que pasa a través del foco $F$ del espejo;
- El rayo que incide en la superficie del espejo paralelo al eje óptico.
Partiendo del rayo que pasa por el centro $C$, puede ver que incide perpendicularmente en la superficie del espejo y, por lo tanto, se refleja a lo largo del mismo rayo.
El rayo que pasa por el foco $F$ se reflejará, por definición, de forma paralela al eje óptico.
El rayo que incide de forma paralela al eje óptico se reflejará en la dirección que pase por el punto focal $F$.
Por lo tanto, se obtiene una imagen que es precisamente la pequeña punta verde clara en la figura. El punto importante, que responde a su pregunta, es que esta imagen no es una imagen virtual: es una imagen real, ya que está ubicada en el plano de convergencia de los rayos, por lo tanto, puede estar invertida. Por el contrario, las imágenes virtuales, que se forman cuando los rayos que salen de un dispositivo óptico siempre se alejan, siempre estarán rectas.
El último punto a abordar es cómo se puede ver esta imagen. Los rayos, después de converger nuevamente en la punta de la pequeña flecha verde clara, se alejan y se dirigen hacia el observador. Por lo tanto, serán los ojos del observador los que tomarán estos rayos divergentes, los enfocarán en la retina y mostrarán al observador la imagen de la pequeña flecha. En este caso específico, la cara del observador es la gran flecha verde (aunque en principio está mucho más lejos del centro $C$ de lo que se representa en esta figura), la pequeña flecha es la imagen invertida de usted mismo que ve en la cuchara
elem
Puntos
35
Es como en cualquier espejo cóncavo. El radio de curvatura de una cuchara es tan corto que tu cara siempre estará más lejos que el centro de curvatura, pero se puede ver lo mismo con un espejo de afeitar si uno se aleja un poco más.
Los diagramas de rayos clásicos no explican muy bien lo que uno ve. Es más esclarecedor tomar el propio ojo como punto de partida para el trazado de rayos (puntos finales de los rayos). Como por ejemplo en este dibujo en Física Conceptual de Hewitt que explica la ampliación de un espejo de afeitar:
Ahora, si el ojo se mueve más lejos, hacia el centro de curvatura, se verá llenando todo el espejo. Los rayos de ida y vuelta están todos en incidencia normal.
Más allá de ese punto, los ángulos se invertirán, y se verá una imagen invertida: la barbilla sobre el ojo, el sombrero debajo. Vea también este video con un espejo grande: https://www.youtube.com/watch?v=K_p5UoD6ljg Presta atención a cómo la cámara se ve a sí misma. (Hay más videos de selfies interesantes con ese espejo en el Exploratorium.)
user621951
Puntos
1
El espejo cóncavo produce una imagen real invertida en una pantalla si se ve erguido detrás de la superficie cóncava, es una imagen virtual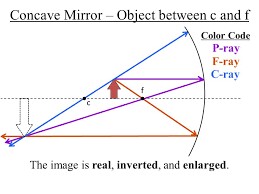
]1
0 votos
¿Por qué crees que la imagen que vemos es virtual y no real?
0 votos
Porque vemos la imagen en la superficie de la cuchara (o espejo)
0 votos
Eso siempre ocurre porque de ahí es de donde provienen los rayos de luz. Eso no hace que una imagen sea virtual.
0 votos
¿Puedes explicar algunos casos excepcionales?
0 votos
No estoy seguro de lo que quieres decir. Ves la imagen en la cuchara porque ahí es de donde provienen los rayos de luz después de ser reflejados. Esto es cierto tanto para imágenes reales como virtuales.