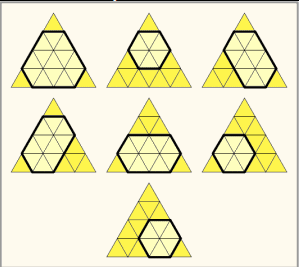
Partiendo de su idea: Por inclusión-exclusión, para $n>3$ $$\tag{1}T_n = X_n +3T_{n-1}-3T_{n-2}+T_{n-3},$$ donde $X_n$ es el número de hexágonos "de tamaño completo", es decir, los que tocan los tres lados. Un hexágono de tamaño completo está determinado por tres enteros positivos $a,b,c$ (los tamaños de los triángulos pequeños cortados) con $a+b<n, b+c<n, a+c<n$ .
¿Cuántas triplas de este tipo ( $a,b,c)$ con $\max\{a+b,a+c,b+c\}<n$ están ahí para cada $n$ ? Vamos a suponer $n\ge3$ . Hay $n-1\choose 2$ posibilidades de elegir $x,y\ge 1$ tal que $x+y<n$ (piense en insertar dos separadores en el $n-1$ lagunas entre $n$ guijarros, agrupándolos así en $x\ge1$ , $y\ge1$ y $n-x-y\ge1$ guijarros). Por lo tanto, hay $n-1\choose2$ triplica cada una de las formas $(1,b,c)$ y $(a,1,c)$ y $(a,b,1)$ . Tenemos que restar el $n-2$ triplica cada una de las formas $(a,1,1)$ , $(1,b,1)$ , $(1,1,c)$ . Entonces tenemos que volver a añadir el triplete simple $(1,1,1)$ . Lo que queda son los triples $(a,b,c)$ con $a,b,c\ge2$ . Al asignar estos a $(a-1,b-1,c-1)$ los biyectamos con el $X_{n-3}$ triples $(x,y,z)$ con $\max\{x+y,x+z.y+z\}<n-2$ . Por lo tanto, $$\tag{2}X_n = X_{n-2}+3{n-1\choose 2}-3(n-2)+1=X_{n-2}+3{n-2\choose 2}+1 $$ Esta sería la cuenta correcta de lo que corresponde a sus (4) y (5). Sin entrar en detalles, vemos que $X_n$ es cúbico en $n$ , no lineal como en tu recuento; así que de ahí viene tu error.
Podemos eliminar $X_n$ mediante la combinación de la ecuación $(1)$ con $n$ y $n-2$ : $$T_n-T_{n-2}=X_n-X_{n-2}+3(T_{n-1}-T_{n-3})-3(T_{n-2}-T_{n-4})+T_{n-3}-T_{n-5},$$ $$\tag{3}T_n = 3T_{n-1}-2T_{n-2}-2T_{n-3}+3T_{n-4}-T_{n-5}+3{n-2\choose 2}+1.$$ Utilizando esta recursión y $T_{-2}=\ldots=T_2=0$ como valores de partida, se encuentra $$ T_3=1\\ T_4=7\\ T_5=29\\ T_6=90\\ T_7=232\\ T_8=524\\ T_9=1072\\ \vdots $$
La ecuación polinómica $x^5=3x^4-2x^3-2x^2+3x+1$ tiene $+1$ como raíz cuádruple y $-1$ como raíz simple. Esto sugiere que existe una fórmula explícita $T_n=a_0+a_1n+a_2n^2+a_3n^3+b(-1)^n$ . Sin embargo, la parte cúbica inhomogénea aumenta el grado, por lo que encontraremos una fórmula explícita $$\tag{4}T_n=a_0+a_1n+a_2n^2+a_3n^3+a_4n^4+a_5n^5+a_6n^6+b(-1)^n.$$ Los coeficientes se pueden obtener al enchufar $(4)$ en $(3)$ y los valores iniciales. Resulta que $$ T_n = \frac{n^6}{480}-\frac{n^4}{192}-\frac{n^2}{80}+\frac1{128}-\frac{(-1)^n}{128}=\frac{4n^6 - 10n^4 - 24n^2 + 15-15\cdot(-1)^n}{1920}.$$