Calcular el centroide de un polígono plano 3D sin proyectarlo en planos específicos

Question

Dada una lista de coordenadas de un plano coplanario ( pt1 , pt2 , pt3 etc.), ¿cómo calcular el centroide del plano coplanario?

Una forma de hacerlo es proyectar el plano sobre el plano XY e YZ, pero no soy muy partidario de este enfoque ya que hay que comprobar primero la orientación del plano coplanario antes de hacer la proyección y calcular el centroide.

Más concretamente, estoy buscando una extensión natural de la Algoritmo del plano centroide 2D en 3D:

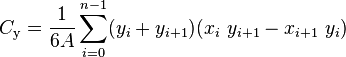
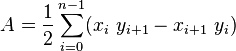
¿Alguna idea?

Answer 1

Se pueden tomar dos vectores ortogonales cualesquiera $\vec{e_1}$ y $\vec{e_2}$ en el avión y utilizarlos como base. También necesitas algún punto $(x_0, y_0, z_0)$ en el plano como origen.

Punto dado con coordenadas $(x_1, y_1, z_1)$ en tu plano calculas sus coordenadas con respecto a la nueva base:

$x = (x_1 - x_0) e_{1x} + (y_1 - y_0) e_{1y} + (z_1 - z_0) e_{1z}$
$y = (x_1 - x_0) e_{2x} + (y_1 - y_0) e_{2y} + (z_1 - z_0) e_{2z}$

Y después puedes aplicar tus fórmulas para obtener $C_x$ y $C_y$ . Estas coordenadas se transforman fácilmente en coordenadas 3D originales:
$x = x_0 + e_{1x} C_x + e_{2x} C_y$
$y = y_0 + e_{1y} C_x + e_{2y} C_y$
$z = z_0 + e_{1z} C_x + e_{2z} C_y$