Evaluar una suma infinita relacionada con$\sinh$

Question

¿Cómo podemos mostrar la siguiente ecuación

PS

Lo encontré en un libro de física (David J. Griffiths, 'Introducción a la electrodinámica', en el capítulo 3, problema 3.48), que no proporcionó ninguna prueba.

Answer 1

Aquí hay una prueba, seguramente no la más simple. Usando$$\frac1{\sinh(n\pi)}=\frac{2e^{-\pi n}}{1-e^{-2\pi n}}=2\sum_{m\text{ odd}}e^{-mn\pi}$ $ y$$2\sum_{n\text{ odd}}\frac{x^n}{n}=-2\ln(1-x)+\ln(1-x^2)=\ln\frac{1+x}{1-x},\qquad |x|<1,$ $ obtenemos$$\sum_{n\text{ odd}}\frac1{n\sinh(n\pi)}=\sum_{m\text{ odd}}\ln\frac{1+e^{-m\pi}}{1-e^{-m\pi}}=\ln\prod_{m\text{ odd}}\frac{1+e^{-m\pi}}{1-e^{-m\pi}}.$$ This is the same as $ \ ln \ frac {G_1} {g_1}$, where $ G_N$ and $ g_N$ are the class invariants as in Chapter 34 of Berndt: Ramanujan's notebooks, Part V. It is known (see same chapter) that $ G_1 = 1$ and $ (g_1G_1) ^ 8 (G_1 ^ 8-g_1 ^ 8) = \ frac {1} {4}$. Hence $ g_1 = 2 ^ {- 1/8} $, y la suma original es igual a$$\sum_{n\text{ odd}}\frac1{n\sinh(n\pi)}=\ln\frac{G_1}{g_1}=\frac{\ln 2}{8}.$ $

Answer 2

esto no es una prueba, GH lo ha dado, pero solo quiero señalar cuatro series más generales de este tipo enumeradas en la extensa colección de Andreas Dieckmann:

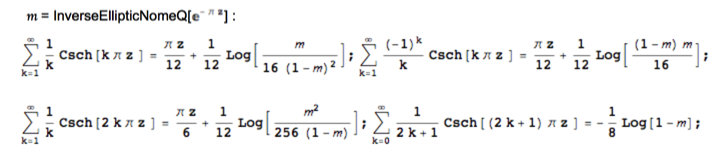
la suma del OP es la cuarta serie (o la diferencia de la primera y la segunda serie) con $z=1\Rightarrow m=1/2$