Pregunta: Para que $d, k \in \mathbb{N}$ existe un algoritmo para determinar si un polinomio de la ecuación de diophantine $$ P(x_1, \dots, x_k) = 0, \ \ \ P \in \mathbb{Z}[x_1, \dots, x_k] $$ del total de grado $d$ en $k$ variables tiene una solución en los números enteros? -- Y para que $d$, $k$ no existe tal algoritmo, respectivamente, se desconoce si dicho algoritmo existe o no?
Observaciones: Desde lineal diophantine ecuaciones en cualquier número de variables puede ser resuelto por medio de un algoritmo, la respuesta es "sí" para toda la $(d,k) \in \mathbb{N}^2$ donde $d = 1$. También, dado que se puede probar si las raíces de un polinomio univariado de cualquier grado son enteros, la respuesta es "sí" para toda la $(d,k) \in \mathbb{N}^2$ donde $k = 1$. Además es bien sabido que la respuesta es "sí" a $(d,k) = (2,2)$. Por otro lado, en la década de 1920 Thoralf Skolem ha demostrado que la respuesta es "no" para $(d,k)$ donde $d \geq 4$ e $k$ es "suficientemente grande", y por el resultado por Zhi Wei Sun, la respuesta es "no" para $(d,k)$ donde $k \geq 11$ e $d$ es "suficientemente grande", cualquiera que sea la mejor conocidos en la actualidad los límites de "lo suficientemente grande" son ... cf. el artículo de Wikipedia sobre Hilbert del décimo problema. Más información se puede encontrar en Andrés Caicedo, la respuesta a estapregunta (aunque en parte en cuanto a soluciones en números enteros no negativos).
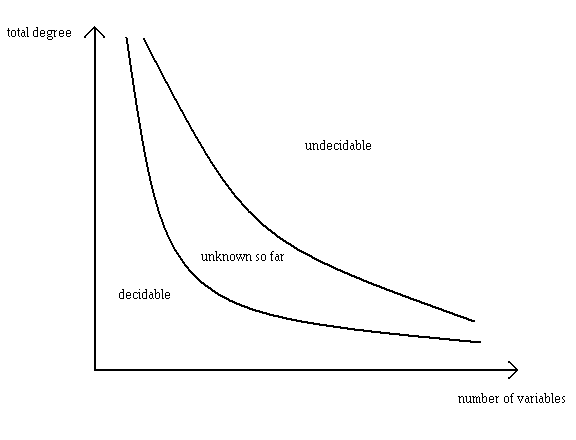
Estos resultados todavía dejan mucho de los casos abiertos, que son lo que en esta pregunta se pide. Una respuesta a esta pregunta podría ser dada en forma de un diagrama como el siguiente, con los límites de la $3$ esbozado áreas a las que se hizo preciso:
Respuesta
¿Demasiados anuncios?Me voy a tomar una puñalada en este. Primero (como se mencionó en Andrés Caicedo, la respuesta a esta pregunta), Siegel demostrado en 1972 que existe un algoritmo para determinar si una ecuación cuadrática en cualquier número de variables tiene una solución, y por lo $(2,k)$ es decidable para cualquier $k$.
A continuación, el caso de $d = 3$ e $k = 2$ es decidable. El más interesante de la situación es el caso de una curva de género, donde Siegel demostrado que hay un número finito de soluciones, y Baker y Coates demostrado en 1970 (en un artículo titulado "Entero puntos en las curvas de género $1$") que es un algoritmo eficaz para encontrarlos. Yo creo que $(1,k)$, $(2,k)$, $(3,2)$ y $(k,1)$ son los únicos casos ahora que se sabe que son decidable.
En particular, el caso de $d = 4$ e $k = 2$ cae en la categoría "desconocido". El caso genérico aquí estaría pidiendo la integral de puntos en un plano de cuarto grado, y (a menos que el avión cuártica es superelliptic), no hay forma sencilla de aplicar Baker lineal de las formas en logaritmos. El mismo problema se plantea para $d \geq 5$ e $k = 2$.
El siguiente caso es $d = 3$ e $k = 3$, que es sin duda en la categoría "desconocido". (Por ejemplo, se desconoce si existen enteros soluciones a $a^{3} + b^{3} + c^{3} = 33$.) Si el $d = 3$, $k = 3$ caso en el que se pueden resolver incluso para homogéneo de ecuaciones, que sería capaz de hacer una $3$-descenso en cualquier curva elíptica sobre $\mathbb{Q}$ y por lo tanto no sería un algoritmo para determinar los grados de curvas elípticas (algo que los demás no sabemos cómo hacerlo).
Encontrar el límite entre lo "desconocido" y "indecidible" es un poco complicado, porque la mayoría del trabajo en indecidible ecuaciones es para aquellos en los que las variables son no-negativos son positivos, lo cual es un poco más fácil. Por ejemplo, Jones, 1982 documento mencionado en Caicedo de la respuesta de las construcciones universal ecuación Diophantine con valores positivos de las variables, con $9$ variables y el grado $\approx 1.6 \cdot 10^{45}$. Sin embargo, para valores enteros de variables, la mejor que se conoce es Zhi Wei Sun $11$ variable de caso (que se encuentra en 1992, con el papel de "Reducción de las incógnitas en Diophantine representaciones"). En el entero positivo es el caso, no son irresolubles Diophantine ecuaciones con $4$ variables y con el grado $58$, $8$ las variables y el grado $38$, $12$ las variables y el grado $32$, etc. No sé de análogos de estos resultados en el entero caso.
¿Dónde está el límite entre desconocidos y indecidible? En Matijasevic y Robinson, 1975 documento donde se prueban la existencia de un universal ecuación Diophantine con 13 variables, dicen: "creemos que el mínimo número de incógnitas es necesario es menor que $13$, posiblemente tan pequeño como $3$, pero los nuevos métodos serán necesarios para obtener el resultado óptimo." Espero que parte de la razón por la que Matijasevic y Robinson cree que el límite puede ser $3$ es que se demostró (en su conjunto 1974 papel en ruso) que dado un polinomio $f(u,v,w,x)$ el problema de determinar si $\exists u, v \in \mathbb{N}$, de modo que $\forall w \in \mathbb{N}$, $\exists x \in \mathbb{N}$ de modo que $f(u,v,w,x) = 0$ es indecidible.
Nota: La conjetura ABC puede o no puede ser un teorema. Si un efectivo de la versión de la Conjetura ABC es cierto, no es (por un resultado de Elkies de 1981, "ABC implica Mordell") un algoritmo para encontrar todos los puntos racionales en curvas, y esto debería dar un algoritmo para todos los casos $(d,2)$ cualquier $d \geq 1$.