¿Por qué los objetos de gran tamaño se rompen fácilmente?

Question

¿Por qué los objetos de gran tamaño se rompen fácilmente? Por ejemplo: si dejo caer una tiza de longitud $L$ desde una altura $h$, entonces existe una mayor probabilidad de que se rompa, en comparación con una tiza de longitud $\frac{L}{2}$ caída desde la misma altura $h$. Y si repito el mismo experimento con la misma tiza después de que se rompe muchas veces, también he observado que después de cierta longitud ya no se rompe en absoluto. Es solo un fenómeno físico que me intriga y que he observado en la vida diaria.

También he observado un fenómeno similar con el vidrio. Por ejemplo, una taza de vidrio se hace añicos en muchas piezas, pero cuando algunas de sus piezas rotas caen desde la misma altura, no se rompen en absoluto. También en este experimento estoy considerando que todos los objetos están cayendo libremente.

Answer 1

Cuanto más grande (y más largo) sea el objeto, más torque experimentará.

Supongamos que la longitud del tiza que tenemos es $\frac{L}{2}$ (Tiza 1) y $L$ (Tiza 2).

Cuando la tiza cae al suelo, es más probable que golpee en uno de sus bordes. Dado que se suelta desde la misma altura, la fuerza sobre la masa más pesada (Tiza 2) será mayor que la enfrentada por la Tiza 1 en uno de sus bordes y además, si consideramos el torque, la Tiza 2 enfrenta más torque que la Tiza 1 en promedio porque el torque es directamente proporcional al producto de su longitud desde su eje de rotación y la fuerza.

Además, el daño de una colisión es aproximadamente proporcional al momento o inercia que es proporcional a la masa y la velocidad y proporcional a su energía cinética, que es proporcional a su masa y al cuadrado de su velocidad.

EDITAR:

1. Acerca de objetos cayendo planos al suelo, la energía potencial del objeto se emplea en romper los enlaces intermoleculares en el sólido. Como los objetos más grandes tienen mayor masa, su energía potencial tiende a ser mayor, por lo que tienden a romper los enlaces que mantienen unido el sólido.

2. Si incluimos la resistencia del aire, entonces es intuitivo que objetos con más masa caigan con más fuerza que un objeto ligero. Dado que los objetos más grandes, en general, son más pesados que los objetos pequeños, podríamos decir que el impulso impartido al objeto más grande es mucho mayor que el impulso impartido al más pequeño. Por lo tanto, probablemente eso pueda explicar por qué los objetos más grandes se rompen con más frecuencia que los más pequeños.

3. Esto es lo que creo que podría ser la respuesta plausible (comparte tus opiniones al respecto): Los objetos más pequeños, en general, tienen más área superficial que volumen (en términos de magnitud). Por lo tanto, los enlaces que mantienen unidos los átomos en la superficie están bien distribuidos, lo que protege bastante bien el interior en comparación con los objetos más grandes. Cuando el objeto cae, debido a la mayor área superficial, la energía transferida al objeto está más dispersa (debido a una mayor relación área superficial a volumen). Una cierta cantidad de energía se dispersa en una superficie mayor, por lo tanto, la densidad de energía no es suficiente para romper las fuerzas intermoleculares. El objeto, en su conjunto, estaría relativamente a salvo ya que para dañar el objeto, primero tenemos que romper la superficie y dado que la superficie protege bastante bien el interior, las cosas están bien para los objetos más pequeños. Así que sospecho que esta sea la razón por la cual, en promedio, los objetos más grandes tienden a romperse con más facilidad.

Al final, todo se trata de cuánta masa tiene el objeto (lo cual depende de su forma y densidad de masa), la relación área superficial a volumen y cuán largo/grande es el objeto. Todo esto contribuye a la gravedad del daño que enfrentan los objetos.

Answer 2

Los objetos grandes se rompen porque son más pesados que los objetos pequeños, por lo que golpean el suelo con más fuerza.

Puede que pienses que un objeto grande también es más fuerte que un objeto pequeño. Eso es cierto, pero no es suficiente para compensar la pesadez.

Para ver por qué, imagina dos objetos de la misma forma, uno con el doble de largo que el otro. Dado que el objeto grande tiene el doble de altura, el doble de ancho y el doble de profundidad, pesará ocho veces más que el objeto pequeño. Pero su resistencia es aproximadamente proporcional a lo grueso que es, el doble de ancho y el doble de profundo. Solo es cuatro veces más fuerte.

J.S. Haldane escribió de manera memorable sobre los animales que caen por pozos mineros: "Una rata muere, un hombre se rompe, un caballo chapotea."

Answer 3

Una de las razones proviene de la estadística de valores extremos. Los objetos se rompen en su punto menos resistente (llamémoslo punto más blando). La probabilidad de tener un punto más blando es mayor en un objeto más grande.

Puedes pensar en una cadena con $N$ eslabones. Cada eslabón tiene una fuerza máxima que puede soportar, $F$. Dado que los eslabones no son todos iguales, $F$ proviene de una distribución de probabilidad, $P(F)$. Entonces la resistencia a la rotura de toda la cadena es el mínimo $F$ entre $N$ valores. Ahora tienes valores $F_1, F_2, ..., F_N$ pero la fuerza total que la cadena puede soportar es el mínimo de esos. Cuanto mayor sea el número de eslabones $N$, mayor será la probabilidad de encontrar un eslabón más débil. La hipótesis del eslabón más débil y la estadística extrema resultante se utilizan ampliamente en la ingeniería mecánica para estimar la resistencia a la tracción de diversos materiales y estructuras.

Si sabes programar un poco, puedes investigar por tu cuenta: arroja $N$ números aleatorios según cualquier distribución y toma el mínimo de estos. Puedes promediar varias ejecuciones independientes, y obtener el valor mínimo promedio de $N$ números aleatorios. Luego observa cómo cambia este valor mínimo promedio con $N$. A continuación, se muestra un pequeño código en Python que hace precisamente eso:

import numpy as np
import pylab as pl

min_N = []
for N in range(10,1000):
    min_current = 0
    for realizations in range(100):
        min_current+=np.min(np.random.rand(N))/100.0
    min_N.append(min_current)

pl.loglog(range(10,1000), min_N)
pl.xlabel('N', fontsize=22)
pl.ylabel('min(N)', fontsize=22)    

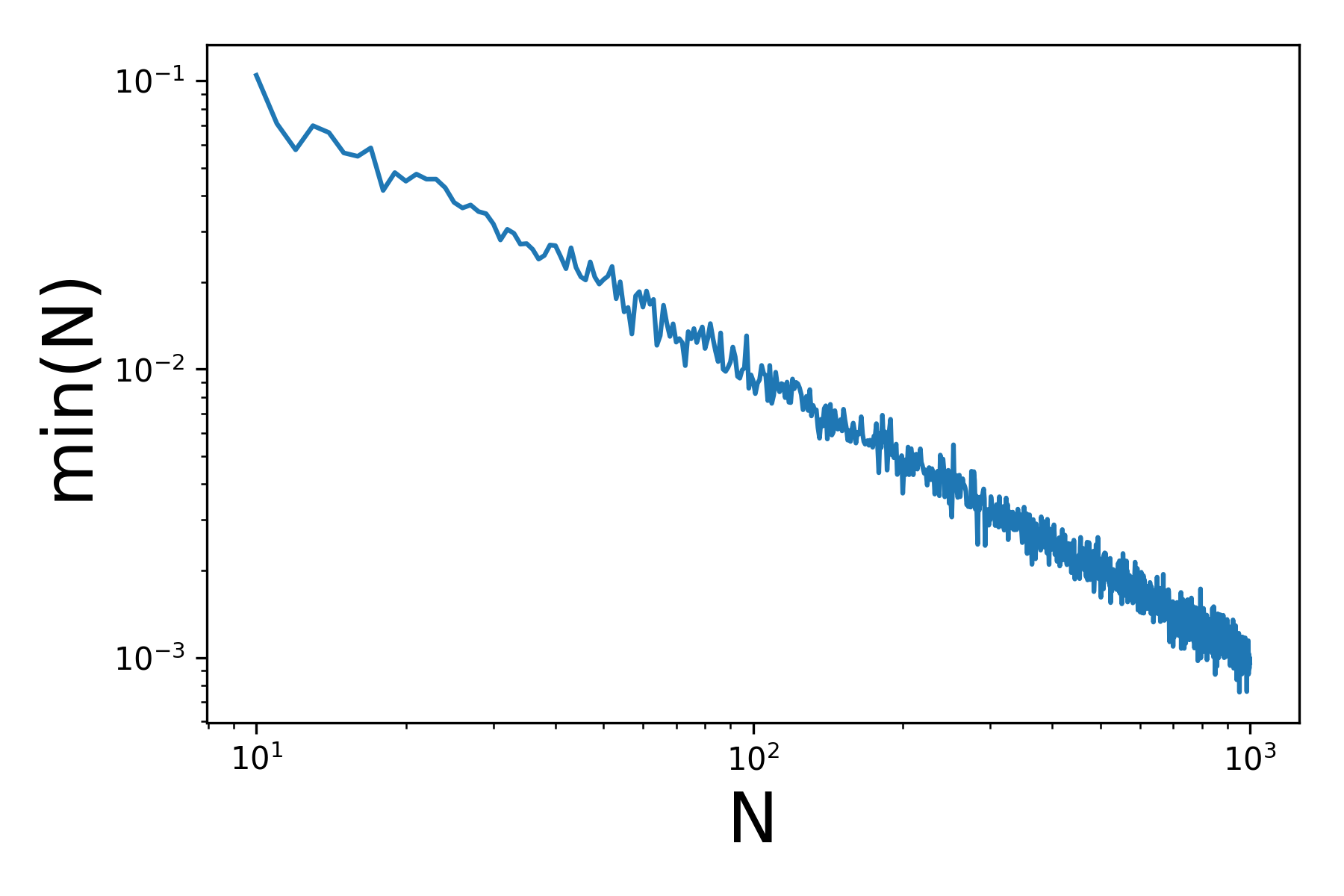
y el resultado:

Ahora puedes ver que el mínimo de $N$ números aleatorios distribuidos uniformemente (es decir, la resistencia de la cadena) disminuye con $N$. Este es un gráfico log-log, por lo que parece que disminuye como una ley de potencias.

Editar: ¿por qué los objetos tienen puntos blandos? Hay múltiples razones:

• Los objetos suelen ser no homogéneos a escala mayor que unas pocas decenas de átomos/moléculas. Los objetos cristalinos tienen defectos como dislocaciones o disclinaciones que provocan campos de estrés no homogéneos en el material; donde el estrés es mayor, el objeto es más blando y tiende a romperse ahí. Los materiales amorfos son heterogéneos por definición.
• Incluso si los materiales fueran completamente homogéneos, la carga externa sobre ellos es heterogénea: un golpe desde el suelo no es una carga uniformemente distribuida en los límites, por lo que dentro del material los esfuerzos serán no homogéneos.
• Finalmente, incluso si la carga fuera distribuida uniformemente en el límite de los objetos, la forma del límite de los objetos es irregular lo que, nuevamente, provoca campos de tensión no uniformes en el material.

Para resumir, la nucleación de la fractura es una interacción de dos efectos: puntos blandos en el material y tensiones no uniformes en todo el material. Esta es la razón por la que los materiales se rompen en diferentes puntos dependiendo de la carga externa que experimentan: un punto podría ser blando (susceptible a romperse, por ejemplo, debido a defectos en el ordenamiento atómico), pero en última instancia depende de la carga (y el campo de tensión no uniforme asociado) si se romperá en ese punto o en otro lugar.

En un modelo simplista, podrías pensar en el material como sitios de red, cada uno de ellos con un esfuerzo de cedencia $\sigma_Y(\vec{r})$ que puede soportar (nota que este esfuerzo de cedencia depende de la posición y está relacionado con la estructura atómica local). Entonces la carga externa (proveniente de un golpe desde el suelo u otra deformación) causa un esfuerzo $\sigma(\vec{r})$ (de nuevo, no uniforme debido a las razones mencionadas anteriormente) en el material. El material se romperá en el lugar donde $\sigma_Y - \sigma$ es el más pequeño (de todos los lugares).

Answer 4

ENFOQUE 1:- El desarrollo de grietas y puntos de rotura allana el camino hacia la rotura. Un proceso importante en la rotura es la propagación de esas grietas y sitios de rotura a través de la estructura del cristal (o la propagación de dislocaciones a través de la estructura del cristal) Ahora, los objetos más grandes tienen más probabilidad de desarrollar arreglos irregulares o más defectos en una dirección en comparación con los objetos pequeños, ya que tendrían un arreglo más largo o más expandido. Por lo tanto, crea más probabilidad de defectos. Como los objetos grandes tienen más defectos, serán más propensos a la propagación de grietas o dislocaciones. Por lo tanto, es más probable que se rompan. Del mismo modo, puedes preguntarte por qué algunos materiales se rompen más que otros. Aquí tienes información adicional para ti:-

ENFOQUE 2:- Ahora hablemos de esto en base a la resistencia a la rotura. Imagina el gráfico de esfuerzo vs deformación. Supongamos que estamos comparando dos objetos (del mismo material pero con diferentes dimensiones). El $Y$ (módulo de Young) será el mismo para ambos. Y la curva después del punto de cedencia hasta el punto de rotura será casi similar para ambos. Entonces, si pudiéramos comparar los puntos de cedencia para ambos objetos, podríamos tener una idea de la resistencia a la rotura. Ahora, $${Y}=\frac{esfuerzo}{deformación}$$ $${Y}=\frac{F/A}{∆L/L}$$ Es obvio que el objeto más grande ejercerá más fuerza sobre el suelo y el suelo también ejercerá más fuerza sobre un objeto grande que sobre un objeto pequeño. Pero también hay un factor {A} (área del objeto). Los objetos más grandes también tienen más área (lo que también tiene en cuenta la resistencia al aire). Entonces, el término de $\frac{F}{A}$ (esfuerzo) es casi el mismo para ambos. Ahora hablando de la deformación; $${deformación}=\frac{∆L}{L}$$ Este ∆L es un cambio muy pequeño para objetos rígidos normales. Ahora, cuando dividimos este término pequeño por $L$, obtenemos un término mucho más pequeño. Ahora para objetos grandes (más largos) L es grande en comparación con los objetos pequeños. Por lo tanto, la deformación neta producida en objetos grandes es menor que en los objetos pequeños. Pero $Y$ es el mismo para ambos objetos (ya que ambos tienen el mismo material). Entonces, para mantener $Y$ constante, el máximo esfuerzo (dentro del cual permanece en el límite elástico) debería ser menor (para el objeto grande) ya que su deformación es pequeña. Por lo tanto, en el gráfico de los objetos grandes, el punto de cedencia se obtendrá a un esfuerzo menor en comparación con el de los objetos pequeños. Muestra que el punto de rotura de los objetos grandes está en una condición de esfuerzo inferior. Por lo tanto, los objetos grandes se romperán fácilmente en comparación con los objetos pequeños. $${esfuerzo} \propto {deformación}$$ Por lo tanto, cuanto menor sea la deformación máxima posible (hasta el límite elástico), menor será el esfuerzo máximo tolerable.

También se puede entender desde la fórmula:- $${\mu} =\frac {{\sigma}^2}{2Y}$$ Donde, $\mu$ es el módulo de resiliencia, ${\sigma}$ es la deformación de cedencia. Esta deformación de cedencia se puede comparar para los dos objetos usando un enfoque similar al que he hecho anteriormente.

Otros conceptos como el torque ya han sido publicados. Así que no me adentraré más en eso.

Answer 5

Los diferentes efectos escalan de manera diferente.

La energía de un trozo de tiza de longitud $l$ soltado desde una altura de $h$ es $mgh$, la cual escala con su masa, la cual escala con el volumen, por lo tanto $E∝l^3$.

La resistencia de un objeto típicamente escalará con su grosor ($∝l$) o su área transversal ($∝l^2$), dependiendo de cómo se rompa.

Así que un trozo de tiza más grande será más resistente, pero tendrá que soportar aún más disipación de energía.