Hay liso de los cuerpos de anchura constante?

Question

El estándar triángulo de Reuleaux no es fácil, pero los tres puntos de tangencial de la discontinuidad puede ser suavizada como en la figura de abajo (a la izquierda), desde el artículo de la Wikipedia. Sin embargo, no está claro (para mí) a partir de este diagrama si la curva es $C^2$ o $C^\infty$.

Meissner del tetraedro es un 3D del cuerpo de anchura constante, pero no es suave, como es evidente en la figura de la derecha a continuación.

   

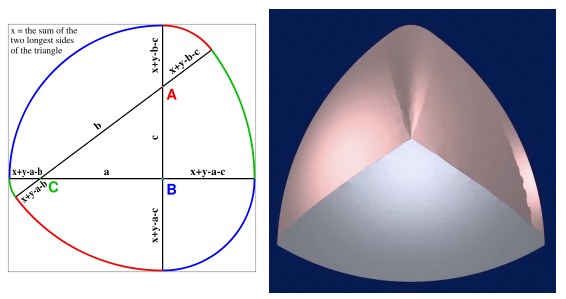
Mi pregunta es:

Hay $C^\infty$ constante de ancho cuerpos en $\mathbb{R}^d$ (otras de las esferas)?

La imagen de Meissner del tetraedro de arriba fue tomada desde el impresionante trabajode Thomas Lachand–Robert y Edouard Oudet, "Los cuerpos de ancho constante en dimensión arbitraria" (Las matemáticas. Nachr. 280, Nº 7, 740-750 (2007); la pre-publicación en formato PDF aquí).

Sospecho que la respuesta a mi pregunta es conocido, en cuyo caso una referencia sería suficiente. Gracias!

Adenda. Gracias a los conocimientos (y rápido!) respuestas por Gerry, Anton, y Andrei, mi pregunta es completamente respondió—estoy agradecido!!

Answer 1

Fillmore mostró que existen conjuntos de ancho constante en $\mathbb R^d$ analítico de límites que tienen un trivial grupo de simetría (por lo que estos son muy diferentes de las esferas; ver "Simetrías de las superficies de ancho constante", J. Diferencial Geom., Vol 3, (1969), pp 103-110).

Por otra parte, el conjunto de los cuerpos de anchura constante con la analítica de los límites es denso en el espacio de todos los cuerpos convexos de ancho constante en $\mathbb R^d$ con respecto a la métrica de Hausdorff (ver, por ejemplo, "aproximación Suave de cuerpos convexos" por Schneider).

Answer 2

Tomar cualquier extraño $C^\infty$-función de $f$ sobre la esfera. Considerar el conjunto convexo $$R_\epsilon=\{\,x\in\mathbb R^n\mid\langle x,u\rangle\le 1+\epsilon{\cdot}f(u)\ \ \text{for any}\ \ u\in\mathbb{S}^{n-1}\,\}.$$ Tenga en cuenta que para todos los suficientemente pequeños $\epsilon>0$, $R_\epsilon$ es un cuerpo liso de ancho constante.

Answer 3

Jay P Fillmore, las Simetrías de las superficies de ancho constante, J Geometría Diferencial 5 (1969) 103-110, dice: la curva de $$x_1=h\cos\theta-{dh\over d\theta}\sin\theta,\qquad x_2=h\sin\theta+{dh\over d\theta}\cos\theta$$ where $h=a+b\cos3\theta$, $0\lt8b\lt a$, is analytic and of constant width. If we rotate this curve in Euclidean space ${\bf E}^n$ about an $(n-2)$-dimensional axis perpendicular to the line $\theta=0$, we obtain an analytic surface, not a sphere, of constant width in ${\bf E}^n$.

El documento puede estar disponible en http://www.intlpress.com/JDG/archive/1969/3-1&2-103.pdf

Answer 4

Este papel se acaba de publicar:

Howard Resnikoff. "En las Curvas y Superficies de Ancho Constante." Abr. 2015. (arXiv abstracto.)

"...ofrecemos una serie de Fourier-basado en la construcción que se produce de forma arbitraria muchas de las nuevas superficies de ancho constante."

---

     

---

Answer 5

Michael Kallay caracteriza el conjunto de todos los conjuntos de planos con un determinado ancho funciones: Ver M. Kallay, la Reconstrucción de un plano convexo cuerpo de la curvatura de sus límites. Israel J. Math. 17 (1974), 149-161. y M. Kallay, Los extremos de los cuerpos, en el conjunto de planos de cuerpos convexos con un determinado ancho de la función. Israel J. Math. 22 (1975), no. 3-4, 203-207.