Conocemos los siguientes aspectos: ∫∞0sinxxdx=∫∞0sin2xx2dx=π2,∫∞0sin3xx3dx=3π8. Además, podemos obtener ∫∞0sin3xx2dx=3log34,∫∞0sin4xx3dx=log2. Entonces, me interesó su generalización.
Pregunta : Dejar p,q∈N ¿podemos simplificar lo siguiente? ∫∞0sinpxxqdx
No tengo ninguna buena idea. ¿Podría mostrarme cómo simplificar esto?
Nota: : Esta pregunta ha sido preguntado anteriormente en math.SE sin recibir ninguna respuesta.

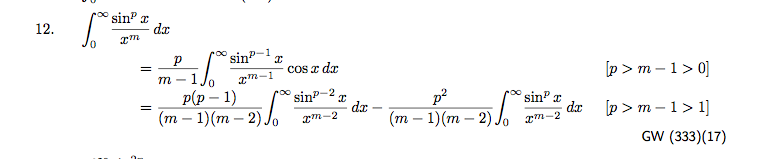


2 votos
math.stackexchange.com/questions/378547 Se puede ampliar la misma técnica para evaluar ∫Rsinm(x)xndx