Esto no es una respuesta, sino una explicación de por qué esta pregunta es tan difícil.
Para números enteros coprimos positivos $a,q$ , dejemos que $$\pi(x;q,a) = \# \{p \leq x : p \equiv a \pmod{q}\}.$$ Para $k \in \mathbb{Z}$ , dejemos que $$A_k = \{n \in \mathbb{N} : \pi(n;8,1) - \pi(n;8,5) = k\},$$ y que $$B_k = \{\pi(n;8,3) - \pi(n;8,7) \in \mathbb{Z} : n \in A_k\}.$$ Entonces su conjetura de que la función $$f(n) = \sum_{p \leq n}{e^{\pi i(p - 1)/4}}$$ es suryectiva en $\mathbb{Z}[i]$ es equivalente a la conjetura de que $B_k = \mathbb{Z}$ para cada $k \in \mathbb{Z}$ .
Para ello, el conjunto $A_k$ debe ser contablemente infinita; es decir, la igualdad $\pi(n;8,1) = \pi(n;8,5)$ debe ocurrir infinitamente a menudo. Este es un resultado difícil, pero de hecho se conoce incondicionalmente: está cubierto por el Teorema 5.1 de " Teoría comparativa de los números primos. II "por S. Knapowski y P. Turán. Al parecer, Jason Sneed ha demostrado ahora incondicionalmente que $\pi(x;q,a) - \pi(x;q,b)$ cambia de signo infinitamente a menudo para todos $q \leq 100$ pero aún no se ha publicado (véase este documento para un debate).
Si se asumen dos conjeturas fuertes, la hipótesis Grand Riemann y la hipótesis de Independencia Lineal (es decir, que las partes imaginarias de los ceros no triviales de todos los Dirichlet $L$ -son linealmente independientes sobre los racionales), entonces se puede decir mucho más. El artículo de Rubinstein y Sarnak sobre Sesgo de Chebyshev muestra que no sólo hay infinitos cambios de signo, sino que la función $$\left(\frac{\log x}{\sqrt{x}} \left(\pi(x;q,a_1) - \mathrm{Li}(x)\right), \ldots, \frac{\log x}{\sqrt{x}} \left(\pi(x;q,a_r) - \mathrm{Li}(x)\right)\right)$$ tiene una distribución logarítmica límite. En concreto, pueden decir aproximadamente la probabilidad $(\log x / \sqrt{x}) \pi(x;8,1)$ y $(\log x / \sqrt{x}) \pi(x;8,5)$ se encuentran en determinadas regiones; por desgracia, esto no dice nada sobre el conjunto $A_k$ para cada número entero $k$ .
Una vez que tenga esa $A_k$ es contablemente infinito, todavía hay que asegurarse de que no hay "conspiración", en el sentido de que el otro número primo raza $\pi(x;8,3) - \pi(x;8,7)$ podría evitar determinadas configuraciones siempre que $x$ es un cero de la carrera de números primos $\pi(x;8,1) - \pi(x;8,5)$ . Esto parece extremadamente difícil, y no sé cómo se podría intentar analizarlo. Dicho esto, Knapowski y Turán estudiaron cuestiones periféricamente relacionadas con esto, así que es posible que haya algo en la literatura que pueda tratar este tipo de problema.
Como apunte, una modificación interesante de esta conjetura es la siguiente. Sea $\chi$ sea un carácter Dirichlet módulo $q$ de modo que $\chi$ está generada por alguna raíz de la unidad $\zeta_Q$ . ¿Es la función $$f_{\chi}(n) = \sum_{p \leq n}{\chi(p)}$$ suryectiva en $\mathbb{Z}[\zeta_Q]$ ?






3 votos
La heurística obvia, que ve esto como aproximadamente un paseo aleatorio, dice que sí.
4 votos
De hecho, hay pruebas numéricas de que los puntos de este paseo "permanecen mucho más juntos" que en un paseo aleatorio. Así, uno podría atreverse a conjeturar que incluso una versión tridimensional de la carrera de los primos es suryectiva, aunque el simple paseo aleatorio en 3 dimensiones no sea recurrente. Pero la heurística es una cosa, las pruebas rigurosas son la otra... .
2 votos
Stefan, ¿puedes dar más detalles sobre estas pruebas numéricas? Según tengo entendido hasta ahora, el paseo de la carrera de números primos está muy bien modelado por un paseo aleatorio típico.
4 votos
@Teo B: El movimiento en sentido negativo y positivo proviene de la carrera de números primos módulo $8$ entre los residuos $1$ y $5$ . Lo más frecuente es que haya más primos congruentes con $5$ modulo $8$ que $1$ . (Para ser específicos, tenemos que hablar de la densidad logarítmica y asumir GRH y LI) La primera vez que los primos congruentes a $1$ modulo $8$ se adelanta en la carrera está entre $10^8$ y $10^9$ .
1 votos
@Teo: Puedes encontrar una introducción elemental al problema de la carrera de primos unidimensional aquí: dms.umontreal.ca/~andrew/PDF/PrimeRace.pdf . Si no me equivoco, hay infinitos cruces de los ejes. El hecho de que la mayor parte de la gráfica esté en un lado del eje vertical procede del sesgo de Chebyshev, véase es.wikipedia.org/wiki/Chebyshev%27s_bias . Esto también distingue el problema de un paseo aleatorio.
1 votos
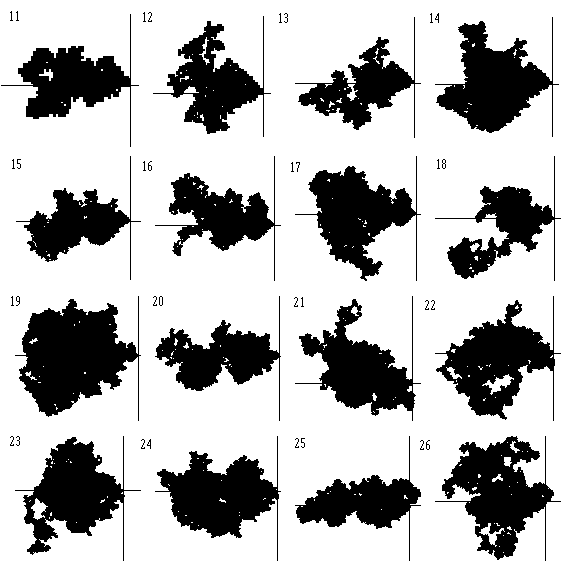
@Greg: He añadido un gráfico de un paseo aleatorio para comparar. No sé ningún resultado en esto, pero sólo se ve diferente ... .
1 votos
Personalmente, no veo nada en las imágenes que sugiera que el paseo de la carrera de números primos sea significativamente diferente de un paseo aleatorio.
0 votos
@Greg: así que crees que el simple paseo aleatorio en $\mathbb{Z}^2$ es un modelo adecuado para la carrera de primos bidimensional(?) -- ¿Puede dar razones para ello?
0 votos
@Greg: Como se ha dicho, no conozco más resultados sobre hasta qué punto un simple paseo aleatorio en $\mathbb{Z}^2$ es un modelo adecuado en este caso. Sin embargo, las propiedades clave del paseo aleatorio son que su comportamiento (es decir, cómo continúa) no depende ni del punto al que ha llegado después de un cierto número de pasos, ni del número de pasos que ya ha dado. He calculado muchas más imágenes que las mostradas arriba, y me parece que la carrera primitiva en 2 dimensiones no comparte ninguna de ellas. (continúa en el siguiente comentario)
0 votos
No sé cómo precisar esto, y en particular cómo excluir que lo que observo son sólo pequeñas distorsiones procedentes de que por condiciones de congruencia fácil $p_i$ mod 8 y $p_{i+1}$ mod 8 no son estadísticamente independientes.
1 votos
Estoy de acuerdo en que, para los primos pequeños, es menos probable que el siguiente primo comparta la misma clase de residuo módulo 8, simplemente porque las otras tres clases de residuo tienen turno primero. Pero este sesgo, y otros similares, desaparecen en el límite. El artículo de Andrew y mío que has enlazado más arriba es un buen punto de partida; también podrías comprobar una conjetura que hago con Feuerverger en nuestro artículo math.ubc.ca/~gerg/index.shtml?abstract=BSRPNR ....
2 votos
Es difícil dar razones concretas por las que la simple $\mathbb Z^2$ (Se puede señalar que la hipótesis generalizada de Riemann implica que la distancia típica desde el origen es del orden de la raíz cuadrada del número de pasos, por ejemplo). Pero me siento confiado en poder desviar cualquier preocupación específica de que deberían ser diferentes, como Eric y yo ya hemos hecho un poco. Siéntete libre de proponer otras preocupaciones.
0 votos
@Greg: bueno -- cuando se ejecuta a través de los primeros 12596957371 primos (es decir, los primos hasta alrededor de $3.206 \cdot 10^{11}$ ), la imagen se mantiene dentro del rectángulo comprendido entre -37501 y 1945 en el eje real y entre -14390 y 16290 en el eje imaginario, mientras que la raíz cuadrada de 12596957371 es aproximadamente 112236. ¿Qué pasa con el factor constante antes de la raíz cuadrada que se espera? --¿Puede ser notablemente menor que 1?
0 votos
@Stefan: No creo que estés normalizando correctamente. Mirando el recuento de primos hasta $3.206\cdot 10^{11}$ esperamos que el término de error en la carrera de números primos esté en torno a $\sqrt{x}/\log x$ o en su caso $$\sqrt{3.206*10^{11}}/\log(3.206*10^{11})\approx 21371.$$
0 votos
@Eric: Pensé que "número de pasos" en el post de Greg significaba "número de primos", ya que los números compuestos no contribuyen. -- Pero en cualquier caso poner en el factor $1/\log{x}$ hace que su aproximación se ajuste bastante bien a las observaciones numéricas.
0 votos
@StefanKohl: Dónde está el paseo aleatorio para comparar, no lo encuentro.
0 votos
@Franky_GTH: Puedes encontrarlo o bien aquí o en el historial de revisiones del post.