Altura de los ladrillos apilados al azar

Question

¿Cuál es la altura esperada de una pila de ladrillos de longitud unitaria, cada uno apilado sobre el anterior con un desplazamiento uniformemente aleatorio dentro de $\pm \delta$ ? La pila se derrumba si el centro de gravedad de la parte superior $k$ hace no se apoye en el ladrillo bajo ese grupo superior. Por ejemplo, aquí he utilizado $\delta = \frac{1}{3}$ y la pila era estable después de el 21º ladrillo fue colocado (los puntos verdes del centro de gravedad del grupo superior), pero el 22º ladrillo hizo que los centros de gravedad se desplazaran (puntos rojos), con el cg de los cuatro ladrillos superiores (flecha marcada) ahora sobrepasando el 18º ladrillo de abajo:
          
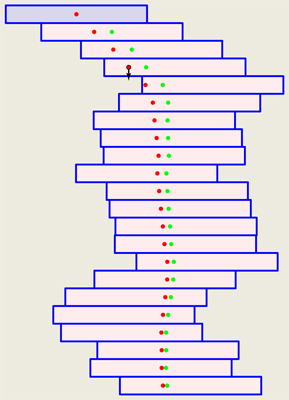
Dejemos que $N(\delta)$ sea la altura esperada (número de ladrillos) de dicha pila. Calcular esto es elemental en cierto sentido, pero no estoy llegando a una formulación satisfactoria que me permita ver claramente el crecimiento global. Tal vez se haya estudiado esto, dada la amplia literatura sobre los voladizos de las pilas de ladrillos? Si es así, se agradecería una indicación.

Me propuse explorar pilas de discos al azar, pero incluso el caso más sencillo de caso de ladrillos rectangulares es más intrincado de lo que preveía.
          
Pido disculpas si todo esto es demasiado elemental.

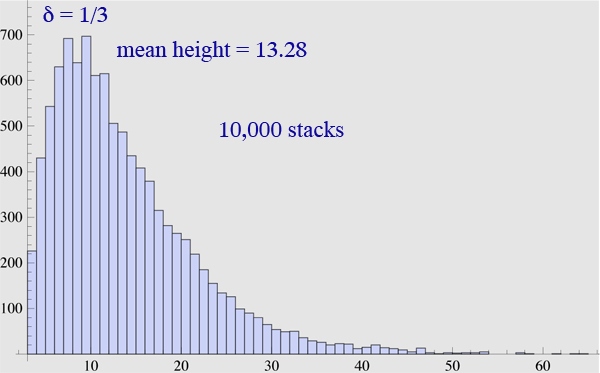
Añadido . Para dar un dato, he aquí un histograma de altura de caída simulada:
          

Actualización . Aquí hay un gráfico de los datos de Aaron Golden, $N(\delta)$ contra. $\delta^{-2}$ , lo que ciertamente apoya a Ori $\delta^{-2}$ conclusión, como señaló JSE:
          

Answer 1

La distribución debe ser aproximadamente geométrica con una expectativa aproximadamente $\delta^{-2}$ . Para atar desde arriba, en cada $2\delta^{-2}$ pasos hay una constante (independiente de $\delta$ ) la probabilidad de que la ubicación del $\delta^{-2}$ El ladrillo estará a una distancia mínima de 3 del primer ladrillo. Entonces hay una probabilidad constante para el siguiente $\delta^{-2}$ ladrillos para estar todos en el desplazamiento 2 o más, causando así el colapso. Este evento puede ocurrir independientemente para cada lote de $\delta^{-2}$ ladrillos, por lo que obtenemos la dominación por la distribución geométrica con la expectativa $O(\delta^{-2})$ .

Por otro lado, la probabilidad de que el centro del ladrillo nunca se desvíe más de $1/4$ lejos del centro para $t$ los ladrillos deben ser más o menos $e^{-ct\delta^2}$ por lo que nos vemos limitados desde abajo por una distribución geométrica con expectativa $\Omega(\delta^{-2})$ también.

El caso de las monedas debería ser similar, aún $\delta^{-2}$ pero con una constante diferente.

Answer 2

Esto pretende ser un comentario a la pregunta, pero carezco de la reputación de MO para dejar comentarios.

Creo que valdría la pena empezar por verificar cuidadosamente que los experimentos numéricos salen correctamente. He escrito un programa rápido para simular el apilamiento que describes y me sale una secuencia de alturas medias:

1.87, 6.10, 13.22, 22.67, 34.65, 48.56, 65.18, 83.94

más de 100.000 pilas para $\delta$ igual a 1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8. ¿Coincide esto con tus resultados? Si no es así, tal vez deberíamos comparar el código fuente.