Atar nudos con bandejas de luz reflectantes

Question

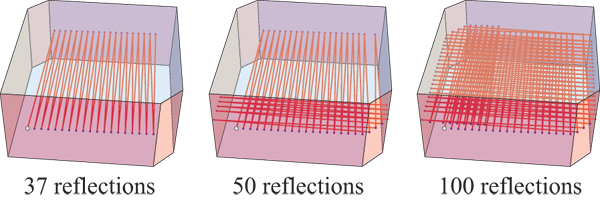
Vamos a un lightray rebote en el interior de un cubo cuyas caras son (interna) de los espejos. Si sus pendientes son racionales, que con el tiempo se forma un ciclo. Por ejemplo, a partir de un punto de $p_0$ en el interior de la $-Y$ frente a un alineado al eje de cubo, y, en principio, en una dirección $v_0=(1,1,1)$, el rayo se vuelva a unir $p_0$ después de 5 reflexiones, formando un hexágono. La siguiente figura muestra una más complicado 16 del ciclo.

          

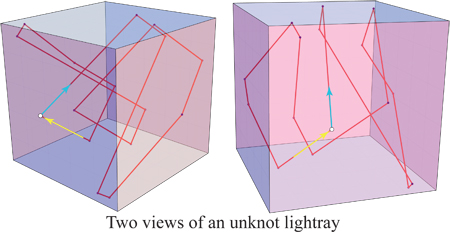
Suponga que $p_0$ e $v_0$ se eligen de manera que (a) el rayo nunca pega directamente en un borde o una esquina del cubo, y (b) la trayectoria del rayo nunca se auto-cruza en el interior del cubo.

Puede cada tipo de nudo ser realizado por un lightray refleja en el interior de un cubo?

La figura anterior es un unknot. Creo (pero no estoy seguro) el 31 de ciclo a continuación se anuda:
          

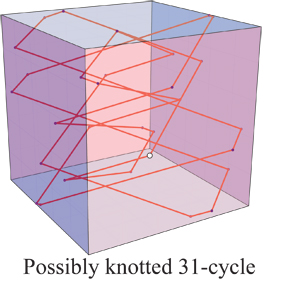
Cualquier anudado ruta de acceso es un palo representación del nudo, pero tal vez los muchos problemas sin resolver en el palo de representaciones no son relevantes para esta situación. Mi pregunta está relacionada con la probabilidad de azar nudos formando en varios modelos, pero por lo general los modelos son dirigido a los polímeros o de ADN. No he visto este modelo lightray explorado, pero estaría interesado en saber de los modelos relacionados.

La elección de $(p_0,v_0)$ permite una gran libertad a "diseño" un nudo, pero parece difícil para el control de la estructura de la ruta para lograr un resultado determinado. He explorado mosaico espacio refleja cubos de modo que el lightray puede ser visto como un segmento recto entre dos imágenes de $p_0$, pero este punto de vista es no ceder me perspectivas.

Si alguien tiene ideas, aunque parcial, me gustaría escuchar de ellos. Gracias!

Edit1 (15Sep10). No he sido capaz todavía de acceso a la Jones-Przytycki papel que Pierre de la cites, pero a sabiendas de la palabras clave que la amabilidad de siempre, yo lo hice encontrar trabajo relacionado por Christoph Lamm ("Hay infinitamente muchos de Lissajous nudos" Manuscripta Mathematica 93(1): 29-37 (1997)) que proporciona información útil:

1. Teorema: Billar nudos en un cubo que son isotópicas para Lissajous nudos.

2. Como dijo Pierre, muchos de los nudos son inalcanzable en estos modelos. En particular, algebraicas nudos no se puede lograr. El resultado técnico es este. Teorema: El Alexander polinomio de billar nudo es un cuadrado mod 2.

3. En 1997, hubo varios intrigante problemas abiertos, incluyendo estas dos. (a) Es cada nudo de billar nudo en algunos poliedro convexo? (b) ¿Puede el unknot lograrse en cada poliedro convexo que soporta el periódico de caminos?

Edit2 (15Sep10). Aquí es un poco más de información sobre los problemas abiertos, ca. 2000, se encuentra en una lista por Jozef H. Przytycki en el libro que resultó de Los nudos en la Hélade '98:

1. Hay un colector que soporta cada nudo? (Por "apoya cada nudo", quiere decir que hay un billar camino isotópicas para cada tipo de nudo.)

2. Hay un número finito de poliedro que soporta cada nudo? Aparentemente no es un "infinito poliedro" que soporta cada nudo.

3. Más específicamente, hay un poliedro convexo que soporta cada nudo? (Este es el 3(a) anterior). [Ver proyecto de Ley de Thurston la corrección de abajo!]

4. Aún más específicamente, es cada nudo apoyado por uno de los sólidos Platónicos?

Yo no he tenido éxito en la búsqueda de información sobre este tema más tarde de 2000. Si alguien sabe más adelante la información de estado, le agradecería un puntero. Gracias por el interés!

Edit3 (5Jul11). La pregunta ha sido contestada (afirmativamente) en un papel por Pierre-Vicente Koseleff y Daniel Pecker recientemente (28Jun11) publicado en el arXiv: "Cada nudo es un billar nudo":

"Mostramos que cada nudo puede ser realizada como un billar de la trayectoria en un convexo prisma. ... El uso de un teorema de Manturov [M], lo primero que demostrar que cada nudo tiene un diagrama que es una estrella del polígono. [...Manturov del teorema nos dice que cada nudo (o link) es percibido como el cierre de un quasitoric trenza...] Entonces, la perturbación de este polígono, podemos obtener un irregular diagrama de un mismo nudo. Podemos deducir que es posible suponer que la 1 y las longitudes de arco de los puntos de cruce son linealmente independientes sobre $\mathbb{Q}$. Entonces, es posible utilizar el clásico de Kronecker densidad teorema para demostrar nuestro resultado."

Edit4 (4Oct11). Un nuevo artículo fue publicado por Daniel Pecker, "del teorema de Poncelet y Billar nudos," arXiv:1110.0415v1. El contexto es que, anteriormente, "Lamm y Obermeyer demostrado que no todos los nudos son de billar nudos en un cilindro," y Lamm conjeturó un cilindro elíptico sería suficiente. Aquí está el resumen:

Deje $D$ ser cualquier elíptica del cilindro derecho. Hemos de probar que cada tipo de nudo puede ser comprendido como la trayectoria de una pelota en $D$. Esto demuestra ser una conjetura de Lamm y le da una nueva prueba de la conjetura de Jones y Przytycki. Utilizamos Jacobi prueba de Poncelet del teorema por medio de funciones elípticas.

Edit5 (13Nov12). El Pecker papel citados anteriormente es ahora publicado: Geometriae Dedicata, De diciembre de 2012, Tomo 161, número 1, pp 323-333.

Answer 1

Estos nudos parecen llamarse nudos de billar en la literatura. Coinciden con los nudos de Lissajous como lo muestran Jones y Przytycki en "Nudos de Lissajous y nudos de billar", Publicaciones del centro de Banach 42, 145-163 (1998). Los nudos de Lissajous son nudos que admiten una parametrización de la forma$(\cos(n_x t + d_x), \cos(n_y t + d_y), \cos(n_z t + d_z))$. Existen fuertes restricciones en tales nudos (ver la wikipedia), y por ejemplo, ningún nudo toro puede ser Lissajous.

Answer 2

Esto empezó como un comentario, pero ya no cabían en el espacio.

Edit1, 3(a) vs Edit2, (3) en su cara de sonido como diferentes preguntas a mí: (forevery nudo hay un poliedro), vs (hay un poliedro tal que forevery nudo) para que el nudo es un billar de la trayectoria.

A partir de una solución a Edit1, 3(a), usted puede obtener un conjunto convexo que funciona como en Edit2,3, pero no veo por qué un poliedro estaría implicado. Si 3(a) es verdadera, entonces tomar una contables de la secuencia de poliedros junto con billar trayectorias que cubrir todos los posibles tipos de nudo. Tomar una secuencia de puntos en $\mathbb {RP}^2$ con distintos barrios de radio $\epsilon_i$. Ahora comprimir el $i$th poliedro por un afín mapa hasta los puntos de contacto con el nudo casi en un par de planos paralelos con la tangente a los planos de manera casi paralela a ese plano, y el injerto esta en a $S^2$ cerca de la pareja de antipodal los puntos que representan el $i$th punto elegido en $\mathbb{RP}^2$.

No es una insinuación de que forevery nudo no es un conjunto convexo ... implica forevey nudo hay un poliedro ... . Un conjunto convexo que trabaja para un nudo, o conjunto finito de nodos, pueden ser modificados para un poliedro: sólo tiene que utilizar los planos tangentes en los puntos de contacto para delinear un poliedro.

Mi conjetura es que: 3(a) es verdadera. Me estoy imaginando a tomar una foto de un nudo como una trenza, y luego la construcción de un convexo tubo sólo para él, donde el nudo en su mayoría rebota hacia arriba y hacia abajo, hacia ti y se aleja de usted, pero en las curvas y cruces donde sea necesario. Si me sale una construcción de hormigón, la voy a llenar de detalles --- en la actualidad es sólo una idea. También me imagino que no hay un único poliedro de trabajo para todos los nudos. Es un reto interesante para tratar de describir las propiedades especiales de los nudos asocia con un poliedro.

Añadido: Plan para la realización de todos los nudos con un poliedro

En más de reflexión (ja, ja), mi conjetura es que se puede construir un único poliedro que se dará cuenta de todos los posibles tipos de nudo. Voy a bosquejar el plan --- los demás son bienvenidos a unirse a cualquiera de relleno, o refutarla.

Actualización: Ver Joseph O'Rourke la respuesta para las fotos.

Para empezar, piense en un plano de polígono que es ligeramente modificada de la plaza. En una plaza, hay trayectorias que rebotan a casi perpendicular a dos paredes paralelas, gradualmente procedimiento de abajo de la longitud. Cuando llegan a la final, vista a través de una pared y el inicio de un viaje de regreso.

Ahora modifique la plaza por biselar una esquina en un ángulo de 45 grados, de modo que cuando las trayectorias de llegar a la corte, de que la huelga en un ángulo de menos de 45 grados desde la perpendicular, así que recurren casi 90 grados y se inicia en la dirección casi perpendicular, con una ligera deriva lejos de la cercana lado. Las trayectorias de rebote de ida y vuelta por un tiempo entre las dos direcciones principales, golpeando el bisel todos otra vez, hasta que alcanzan el final de la bisel, cuando comienzan un viaje crisscorssing entre el segundo par de lados paralelos.

Dicho de otro 45 grados de bisel en la esquina opuesta, por lo que ahora hay trayectorias periódicas con esta descripción cualitativa con arbitrariamente muchos cruces entre pares de lados paralelos.

Tengo un fuerte presentimiento de que cualquier tipo de nudo se pueden organizar en un formulario que tiene proyección a una de estas trayectorias, sólo hacer uso de la principal tejido de la parte para crear el tipo de nudo, pero no he pensado en los detalles. Supongamos que es así, o al menos se supone que tenemos un nudo que tiene un tejido de estilo de la proyección.

Ahora, hacer un cilindro con el hexágono como el anterior como base, la adición de dos nuevas caras perpendiculares a las caras del cilindro. Lo mejor es visualizarlo como una placa delgada, aunque lógicamente es irrelevante cómo de alta es. Trayectorias en el cilindro mapa de trayectorias en el hexágono. Para cada trayectoria cerrada $\gamma$ en el hexágono y para cada entero $N$, hay un círculo la pena de trayectorias en 3 dimensiones que se proyectan a $\gamma$ y golpeó el suelo y el techo exactamente $N$ veces (a intervalos regulares). El extra círculo parametrizes su fase.

Lema : para cualquier $\gamma$ y cualquier especificación de cruce de información, hay una sala de billar de la trayectoria que los proyectos a $\gamma$ y ha determinado los tipos de cruces.

Sospecho que esto es probablemente reflexiva de conocimientos a un grupo de matemáticos. Es decir que si usted toma una colección de $H$ de los números en el intervalo (las alturas verticales), y luego mirar su órbita en virtud de la semigroup $\{ N x + b\}$ generado por las traducciones y la multiplicación por números enteros, entonces el orden de diente de sierra(Nx + b)(H) puede ser cualquier cosa. Creo que más fuerte de hecho es cierto que las imágenes deben ser denso en el conjunto de la $|H|-tuples$ en el intervalo.

Si este plan se sostiene, entonces cada tipo de nudo puede realizarse en este 8 de cara poliedro.

Answer 3

Este es mi entendimiento de la Ley de Thurston la ingeniosa idea:
          
He seleccionado la inicial de rayos a la deriva lentamente hacia arriba, y no de ejecutar la simulación tan lejos como se reflejan en el techo.

Según el proyecto de Ley de la petición, aquí es una vista aérea de la derecha de la imagen anterior, con rayos de colores para distinguir más claramente refleja los planos.
          

Answer 4

Volviendo a la sawteeth descrito por Bill: muchos (o todos) los patrones de cruce puede ser generado si los parámetros x de los cruces son racionalmente independiente (o 'lo suficientemente independiente'). En particular, las simetrías en los x-y-sombra debe ser evitado.

Un artículo de la mina 'de Fourier nudos' aborda la cuestión de si ciertas billar curvas en 2 dimensiones permiten la construcción de todos los nudos si el z-movimiento es arbitraria (me voy a centrar en el cuadrado y el círculo). Voy a enviar este artículo a cualquiera que esté interesado (el 5 página artículo es de 1998 y parte de mi tesis doctoral, que es la razón por la que no se publica en otros lugares).

Mi favorito de la sala de billar para generar todos los nudos es el prisma a través de cualquiera de la elipse. En este caso la x-y-caminos son asimétricos suficiente, pero sería necesario demostrar que las coordenadas de los cruces son, por ejemplo, racionalmente independiente. - Christoph Lamm