Aquí es una idea. Considere la siguiente parametrización, que se supone que cubre el espacio de configuración en cuestión.
$$\mathcal{C}_7:=\left\{\pmatrix{x_k\\y_x\\z_k},\pmatrix{a_k\\b_k\\c_k}_{1\leq k\leq 7}\in{\mathbb{R}^{3\times 2}}^7\,\middle |\, \text{such that conditions 1.-4. are satisfied} \right\} $$
Condiciones:
- $x_k^2+y_k^2+z_k^2=1$
- $\left\langle\pmatrix{x_k\\y_k\\z_k},\pmatrix{a_k\\b_k\\c_k} \right\rangle=0$
- $a_k^2+b_k^2+c_k^2=1$
- $d(l_i,l_j)\geq 2$ para $1\leq i<j\leq 7,$ donde se define la línea de
$$l_k:=\left\{2\pmatrix{x_k\\y_k\\z_k}+\alpha\pmatrix{a_k\\b_k\\c_k}\,\middle|\,\alpha\in\mathbb{R} \right\}$$ and denote with $d(\cdot,\cdot)$ la distancia entre dos líneas.
Tenga en cuenta que la condición 4. puede ser reescrito como polinomio desigualdades. Por lo tanto $\mathcal{C}_7$ es un semi-algebraicas conjunto en $\mathbb{R}^{42}$.
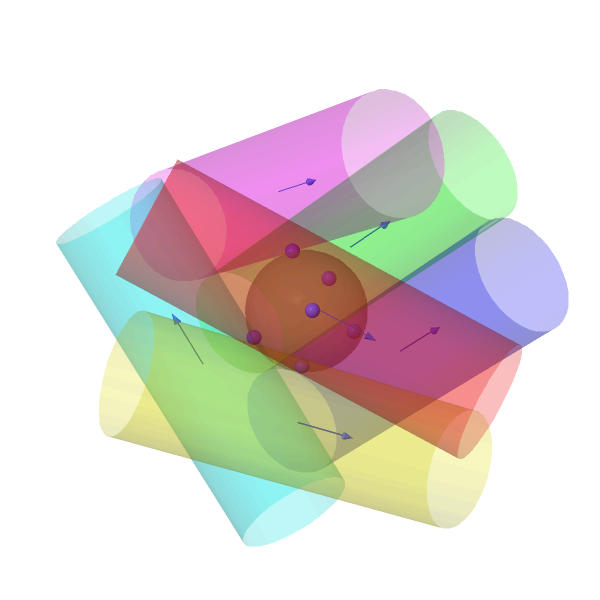
El $(x,z,y)$ son los puntos, en donde la unidad de cilindro es tangente a la unidad de la esfera. El correspondiente $(a,b,c)$ da la dirección en el espacio de la tangente y de las líneas de $l$ son los núcleos de los cilindros. (Tenga en cuenta que $(-a,-b,-c)$ da el mismo cilindro.)
A la pregunta "Es $\mathcal{C}_7$ vacío?" debe ser decidable. Tal vez una aproximación algorítmica podría ayudar desde aquí.
Para las otras preguntas que el estudio de un análogos definidas $\mathcal{C}_6$, lo cual sabemos no puede ser vacío podría ser vale la pena.
Yo escribí un pequeño programa que intenta encontrar puntos de la semi-algebraica de conjuntos. Esto es lo que encontrado por $\mathcal{C}_6$ (haga clic aquí para ver una animación).
![6 kissing cylinders]()
Vamos a tomar un punto de vista ligeramente diferente. Fijar el radio de la bola de a se $1$, pero vamos a los radios de las $k$ cilindros variar mientras se asegura de que todos los cilindros tienen el mismo radio. Entonces podemos preguntar: ¿Cuál es el mayor radio de $r_k$, por lo que nos podemos encontrar en $k$ no se solapan los cilindros de radio $r_k$, que
toque la unidad de la bola? Por lo tanto la pregunta es: $r_7\geq 1?$
Un evidente límite inferior en $r_k$ proviene del embalaje que permite que una sección ecuatorial que es un círculo de embalaje, como por $k=6$ en la figura 1 y la figura 2 en la pregunta del post. Por tanto, tenemos:
$$r_k\geq \frac{\operatorname{sin}(\frac{\pi}{k})}{1-\operatorname{sin}(\frac{\pi}{k})}$$
Aquí está una lista de aproximaciones decimales para las pequeñas $k$s:
$$\begin{array}{c|cccccc}k&3&4&5&6&7&8\\\hline
\frac{\operatorname{sin}(\frac{\pi}{k})}{1-\operatorname{sin}(\frac{\pi}{k})}
&6.464101& 2.414213& 1.425919& 1&
0.766421& 0.619914\end{array}$$
Tal vez sorprendente resultado de mis cálculos es el hecho de que $r_6>1$, de hecho
$$r_6> 1.04965$$
Así que en otras palabras es la configuración de $6$ cilindros donde los cilindros de radio mayor que $1.04965$. Aquí está una foto de la configuración
(de nuevo, haga clic aquí para ver una animación):
![6 kissing cylinders]()
También me atrajo cilindros de radio $1$ con la misma tangente puntos, por lo que se puede ver la diferencia.
El espacio de configuración puede ser visto como subconjunto de la $6$la potencia de la unidad de la tangente paquete de la esfera $(T^1(S^2))^6$ (ver condiciones 1.-4. y Henrik Rüping del comentario).
El resultado de la búsqueda de una configuración con un amplio radio es: el espacio de configuración contiene un subconjunto abierto de $(T^1(S^2))^6$ y por lo tanto es $18$-dimensiones localmente.
Editar:
Aquí está la lista de los límites inferiores en $r_k$ para las pequeñas $k$:
- Para $k=3$ e $k=4$ I conjetura de la trivial obligado para $r_k$ dado anteriormente a ser fuerte.
- Para $k=5$ uno puede encontrar una configuración que se muestra:
$r_5>1.45289>1.425919$
- Para $k=6$ tenemos $r_6>1.04965 >1$ como se mencionó anteriormente.
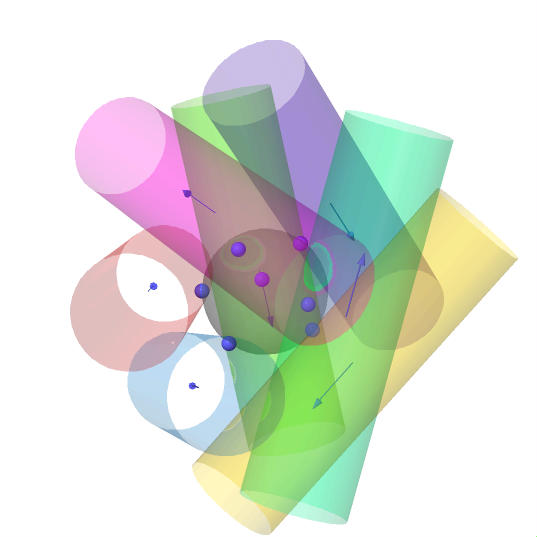
- Para $k=7$ he encontrado una configuración que muestra $r_7>0.846934>0.766421$. Aquí está una foto de esta configuración (de nuevo, haga clic aquí para ver una animación):
![7 kissing cylinders]()
