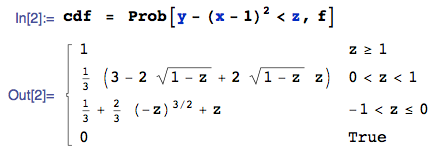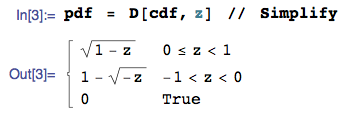Aunque su fórmula final es correcta (kudos para eso), me deja abogan por un enfoque más sistemático. Se advierte sin embargo, que este enfoque evita casi todos de la cabeza-arañazos, por lo tanto no es adecuado para alguien que prefieren este tipo de experiencia (es decir, de la cabeza rascarse) a lo banal de la aplicación de algunos de rutina y muy seguro de procedimiento.
Primer paso: anote la densidad correctamente.
Que es, recordemos que la densidad de $f$ de la distribución de $(X,Y)$ está definida en todo el espacio $\mathbb R^2$ por lo tanto, uno debe definir la función de $f$ en todas partes y evitar los casos. Esto es fácil de hacer, utilizando funciones de los indicadores. Aquí, para cada $(x,y)$ en $\mathbb R^2$,
$$
f(x,y)=\frac12\mathbf 1_{0\leqslant x\leqslant 2,0\leqslant y\leqslant 1}.
$$
Segundo paso: Utilizar el enfoque funcional.
Es decir, tratar de llegar a la identidad
$$
E[u(Z)]=\int_\mathbb R u(z)g(z)\mathrm dz,
$$
para cada acotado medible función de $u$. Si esto se hace, uno sabe que $g$ es la densidad de $Z$.
Para ello, tenga en cuenta que, por definición de la distribución de $(X,Y)$ como la medida de la densidad de $f$,
$$
E[u(\color{red}{Y-(X-1)^2})]=\iint_{\mathbb R^2} u(\color{red}{y-(x-1)^2})f(x,y)\mathrm dx\mathrm dy,
$$
por lo tanto el objetivo es equiparar la RHS de los dos últimos muestran las ecuaciones. Tenga en cuenta que nada de lo que escribí hasta ahora es el caso específico de ahí que estos pasos siempre será el mismo (aburrido, me dije).
Tercer paso: Elegir un cambio de variable.
Aquí, $(x,y)\to(z,t)$ donde, obviamente, $z=\color{red}{y-(x-1)^2}$ e $t$ es casi gratis. Una opción plausible es $t=x-1$ (pero otros son igualmente útiles). Este es el primer momento en que uno debe ser un medio despierto.
Uno debe expresar también el antiguo variables $(x,y)$ en términos de las nuevas variables $(z,t)$ (segunda mitad despierto momento). Aquí, $(x,y)=(t+1,z+t^2)$.
Cuarto paso: Continuar con el cambio de variable mediante el cálculo de la Jacobiana asociada.
Aquí, $\mathrm dx=\mathrm dt$ por lo tanto $\mathrm dx\mathrm dy=\mathrm dt\mathrm dz$, por lo tanto el Jacobiano (tercio medio despierto momento) es $1$ y
$$
E[u(Z)]=\iint_{\mathbb R^2} u(z)f(t+1,z+t^2)\,1\,\mathrm dz\mathrm dt,
$$
lo que indica que
$$
g(z)=\int_\mathbb Rf(t+1,z+t^2)\mathrm dt,
$$
es decir, en el presente caso,
$$
g(z)=\int\frac12\mathbf 1_{0\leqslant t+1\leqslant 2,0\leqslant z+t^2\leqslant 1}\mathrm dt=\frac12\int_{-1}^1\mathbf 1_{-z\leqslant t^2\leqslant 1-z}\mathrm dt.
$$
Ahora la identificación de $g$, que en general es bastante rápido, pero en su caso es realmente tedioso. Uno tiene:
- Si $z\gt1$,, a continuación, $t^2\leqslant 1-z$ nunca sucede.
- Si $0\lt z\lt1$,, a continuación, $-z\leqslant t^2\leqslant 1-z$ e $-1\lt t\lt1$ pasa al $-\sqrt{1-z}\leqslant t\leqslant\sqrt{1-z}$.
- Si $-1\lt z\lt0$,, a continuación, $-z\leqslant t^2\leqslant 1-z$ e $-1\lt t\lt1$ pasa al $-1\leqslant t\leqslant-\sqrt{-z}$ o $\sqrt{-z}\leqslant t\leqslant1$.
- Si $z\lt-1$,, a continuación, $-z\leqslant t^2$ e $-1\lt t\lt1$ nunca sucede.
Esto demuestra que
$$
\color{verde}{g(z)=\sqrt{1-z}\,\mathbf 1_{0\lt z\lt1}+(1-\sqrt {z})\,\mathbf 1_{-1\lt z\lt0}}.
$$
Paso Final: Comprobar que el resultado es plausible en todas las maneras que usted puede pensar.
No omita este paso final. Aquí, comprobar al menos que $g\geqslant0$ en todas partes y que la integral de $g$ a $\mathbb R$ es $1$ (de lo contrario, algo salió mal). Et voilà!
