¿Qué tipo de sistema ejemplos de local indicador de la transformación y de la intensidad del campo-como objetos?

Question

Esto es esencialmente un seguimiento motivado por esta respuesta a mi pregunta sobre el medidor de transformación de la interpretación de los tipos de identidad.

Un campo $$\psi:\mathcal M\to\mathbb C^n$$ es una sección de la $\mathbb C^n$-paquete sobre el espacio-tiempo colector $\mathcal M$. Tenemos un local de calibre transformaciones $$\psi(x)\mapsto \psi'(x):=U(x)\,\psi(x)\ :\ (\mathcal M\to \mathbb C^n)\to(\mathcal M\to \mathbb C^n).$$

Ahora considere la posibilidad de un idioma con el tipo de polimorfismo y la clase $M$ de todos los tipos de cuyos elementos se pueden poner en una lista. Deje $\Psi$ ser polimórfico, función que, para cada tipo de $X\in M$, se asigna una $X$-lista a un número entero, es decir, de su longitud. Por ejemplo, el uso de Haskell sintaxis, si $X=\mathrm{Bool}$,, a continuación,$\Psi_\mathrm{Bool}\left([\mathrm{True},\mathrm{True},\mathrm{False}]\right) = 3$. En el Sistema F notación, tenemos

$$\Psi:\forall X.\left([X]\to\mathrm{Int}\right).$$

El medidor de transformaciones debe corresponder a los mapas

$$u\ :\ \forall X.\left([X]\to\mathrm{Int}\right)\ \longrightarrow\ \forall X.\left([X]\to\mathrm{Int}\right).$$

Yo podría venir para arriba con algunas $u$'s, por ejemplo, la asignación de la función length $\Psi$ a un mapa de $\Psi':=u\,\Psi$ que, por el contrario devuelve 42 veces la longitud de una lista. Pero eso sería, en términos de la física, una de calibre global de transformación, porque no es sensible al tipo $X$. Creo que, dado que el único invariante de un número finito de dimensiones de espacio vectorial es su cardinalidad, no debería ser posible construir un local de transformación en este caso. ¿Cuál sería un ejemplo práctico para un local de calibre transformación en este sentido?

Por otra parte, yo quería dibujar una vida paralela a tipos de identidad. Bueno en primer lugar, hay el menor obstáculo que la transformación no puede ser dada por una expresión en la mayoría de los idiomas, de los tipos generalmente no son objetos de primera clase. Supongo que esta elección de diseño está hecho porque de lo contrario el tipo de inferencia sería echado a perder. En homotopy tipo de teoría que tiene la realización de "los tipos son términos demasiado" (a través de la n-categorías?) y, a continuación, es posible. Pero, en cualquier caso, todavía no puedo precisar la especificación cuando un tipo es una identidad de tipo. Entiendo que la "identidad" para homotopy equivalente espacios y invariante gauge Lagrangians, pero hay no-estructuras geométricas, específicamente la programación relevantes, que se comportan de idéntica antes y después de la transformación?

edit: ahora hice dos visualización del ejemplo aquí y luego:

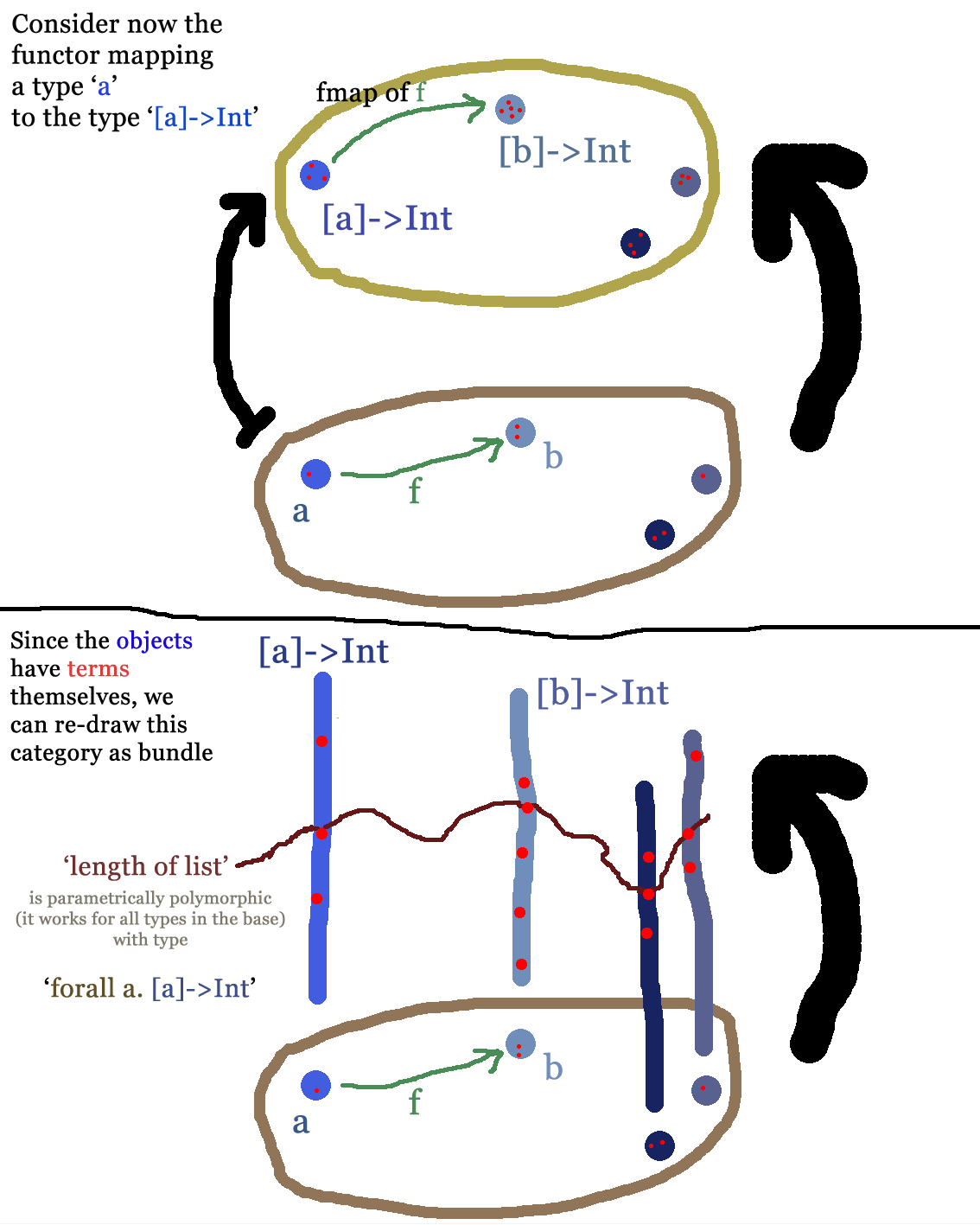
La pregunta entonces es ¿qué un sensible indicador de la sección en la segunda pic sería. (También he hecho dos imágenes más que va más allá de lo que se preguntó: natural de las transformaciones y de las mónadas como en Haskell.)

Por cierto., Sé que HoTT no aplicar tipos de dependientes, no "sólo" de forma paramétrica polimórficos, pero eso no debería ser un obstáculo.

Answer 1

Hay un montón de diferentes aspectos planteados en la pregunta. Voy a tratar de dar algunas indicaciones. Pero me doy cuenta de que la relación de esta pregunta reales de la física no es muy fuerte, en lugar de la pregunta, parece ser más general, después de conseguir una sensación para los tipos de identidad en homotopy tipo de teoría (HoTT). Me imagino que hay otros grupos de discusión más adecuado para este tipo de cuestiones, por ejemplo en el grupo de Google con la (discutible lamentable) título "HoTT aficionados" que usted podría pensar acerca de la publicación de preguntas.

Ahora, con respecto a las preguntas, brevemente pasando a través de él de arriba a abajo:

en primer lugar, un mapa de $\mathcal{M} \to \mathbb{C}^n$ es $\mathbb{C}^n$valores de la función en $\mathcal{M}$. Uno puede considerar esto como una sección de una $\mathbb{C}^n$-haz de fibras de más de $\mathcal{M}$, sí, pero que luego sería el trivial tales haz de fibras.

(Secciones de no.trivial de los paquetes pueden ser codificados en HoTT mediante el uso de tipos de dependientes. Si desea aprender más acerca de esto, hágamelo saber y voy a ampliar).

A continuación, con respecto a la auto-equivalencias del tipo de funciones de las listas de los números naturales: de hecho, supongo que esto no tiene muchas auto-equivalencias. Si uno puede considerar no natural de números, pero los números enteros, entonces no habría algunas obvias (es decir, añadir +1 a cada función, cuya inversa sería la operación que agrega -1).

A continuación, respecto a la pregunta de cómo identificar un tipo de identidad: uno no mira a un tipo arbitrario y pregunte "¿Es este un tipo de identidad?" (Se puede hacer esto, pero no creo que eso es lo que está después.) Es más bien que para un determinado tipo, a continuación, se construye la identidad correspondiente tipo. (Observe también que el tipo de identidad de algún tipo $X$ es $X \times X$-dependientes tipo. )

Dado el tipo de preguntas de arriba, a mí me parece que las aplicaciones de la física no está tanto en el enfoque, como es conseguir una sensación básica para homotopy tipo de teoría como tal. Para ese propósito, supongo que no hay nada mejor que trabajar a través de la HoTT libro. (Supongo que eso ya lo sabes, pero me dejó re- destacar de todos modos.)