¿Puede alguien ver una buena forma de visualizar el SPD cono de 3x3 matrices simétricas? Estoy interesado en algo que destacar es la estructura especial, como la no-uniformidad.
He aquí un intento, se ve muy suave para mí
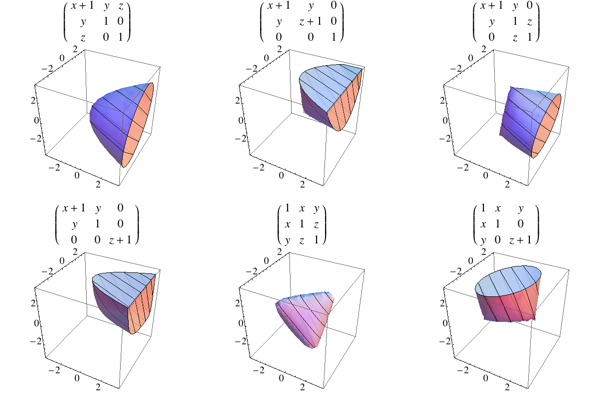
¿Puede alguien ver una buena forma de visualizar el SPD cono de 3x3 matrices simétricas? Estoy interesado en algo que destacar es la estructura especial, como la no-uniformidad.
He aquí un intento, se ve muy suave para mí

Creo que el "simétrico" proyecciones a tres dimensiones hacen un trabajo bastante bueno. Si usted complot en contra de la diagonal entradas, $\begin{bmatrix}x & 0 & 0 \\ 0 & y & 0 \\ 0 & 0 & z\end{bmatrix}$, usted consigue tres nonsmooth bordes a lo largo de los ejes de coordenadas. Con las entradas fuera de la diagonal, $\begin{bmatrix}1 & x & y \\ x & 1 & z \\ y & z & 1\end{bmatrix}$, obtendrá cuatro nonsmooth los vértices de un tetraedro forma en las coordenadas $(\pm1,\pm1,\pm1)$.
 $\quad$
$\quad$ 
Cualquier punto en el que el límite es nonsmooth corresponde a una matriz con más de una fuga autovalor. Esto es fácil de comprobar por la nonsmooth puntos en estos dos casos en particular.
(P. S. Para el beneficio de las futuras búsquedas de los usuarios, creo que la frase "cono de positivo semidefinite matrices" debe aparecer en algún lugar de esta página :) ...)
I-Ciencias es una comunidad de estudiantes y amantes de la ciencia en la que puedes resolver tus problemas y dudas.
Puedes consultar las preguntas de otros usuarios, hacer tus propias preguntas o resolver las de los demás.