Quiero saber por qué los copos de nieve (y otros cristales) crecen simétricamente y encuentro que la respuesta principal a la pregunta establecida es totalmente insatisfactoria.
Cuando el agua se congela, obtienes hielo. El hielo, como muchos materiales sólidos, forma una estructura cristalina. En el caso del agua, la estructura cristalina se puede atribuir al enlace de hidrógeno, un tipo especial de interacción atractiva.
Entonces, un gran trozo de hielo tendrá una estructura cristalina, con direcciones preferidas, simetría translacional y algunas simetrías rotacionales.
La naturaleza agrega una molécula de agua a la vez. Las moléculas siempre intentan elegir la posición más favorable desde el punto de vista energético en el cuerpo congelado. Debido a que estas leyes de creación de un copo de nieve son simétricas con respecto a las simetrías rotacionales, se sigue que cualquier simetría que exista al principio, como la simetría hexagonal de un pequeño número de moléculas en el cristal inicial, se preservará.
No, lo siento, no tiene sentido en absoluto. Falta algo enormemente importante en esta respuesta: la causalidad.

Supongamos que en un momento determinado el copo de nieve es perfectamente simétrico. Luego supongamos que una molécula aleatoria se agrega en el punto A. Para mantener la simetría, más tarde se agrega una molécula aleatoria en un punto correspondiente B (y otros cuatro). Pero el movimiento de la molécula de agua es aleatorio y no hay razón para que termine en B o en cualquier otro lugar en particular.
Incluso considerando los comentarios de theo sobre el crecimiento dendrítico, ¿por qué no vemos esto?
No veo absolutamente ninguna razón por la cual una molécula de agua adicional en un momento dado no pueda aterrizar en una posición energéticamente desfavorable. Además, si las consideraciones de baja energía fueran una fuerza impulsora, los copos de nieve serían aproximadamente esféricos.
Entonces, ¿qué está realmente sucediendo? ¿Cómo puede una protuberancia en A crear una fuerza atractiva en un punto distante B?

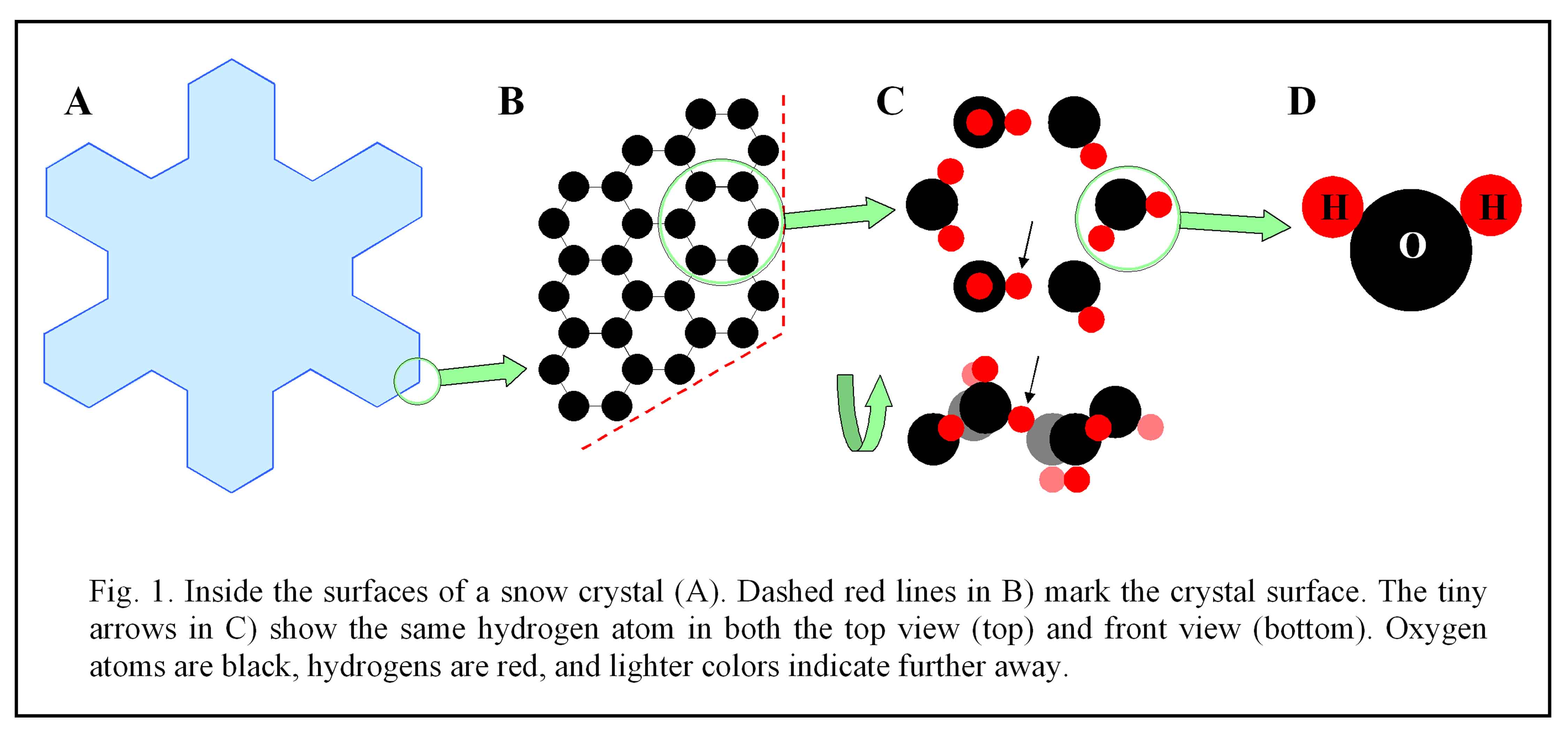

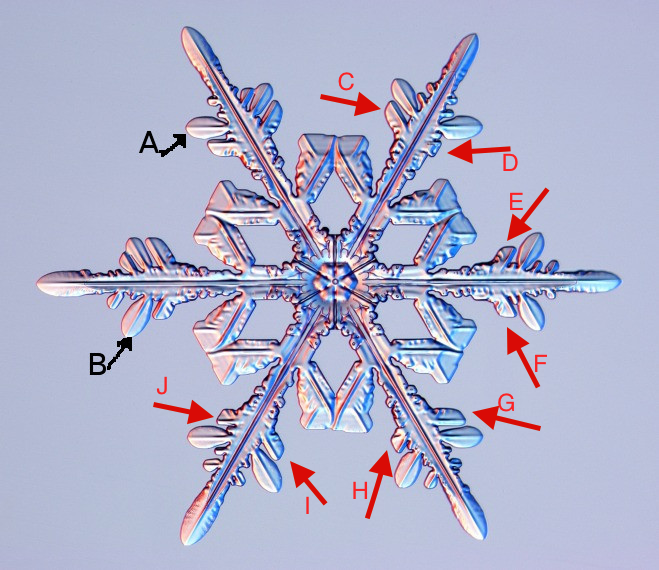


1 votos
Parece, después de analizar las diversas respuestas, que la "causalidad" que estás buscando ¡es el fotógrafo! Al "seleccionar" el copo de nieve más simétrico para fotografiar, hace que el resto de nosotros creamos que "todos" los copos de nieve son "altamente" simétricos, naturalmente.
3 votos
Entiendo que la selección está ocurriendo, pero cálculos breves me hacen escéptico. Supongamos que dividimos cada uno de los brazos principales en mi esquema en 10 segmentos, todos los puntos dentro de cada sección siendo "equivalentes" para los fines de la simetría. Los brazos secundarios tienen 10 puntos de sujeción candidatos, y suponer que un brazo secundario en cada lado de cada brazo principal, da 10121012 permutaciones de esta forma básica. ¿Alguien realmente buscó tantas para encontrar la que está en la foto?