Transformaciones geométricas y límite (pi = 4 revisitado !!)

Question

Considerar tres transformaciones geométricas.

1º: La geométrica de la "prueba" de que la hipotenusa de un triángulo rectángulo es igual a la suma de los cuadrados de los otros lados. El enlace está aquí.

2º: El famoso "pi=4" "a prueba" por la transformación geométrica

3º: Arquímedes del método de cálculo de pi

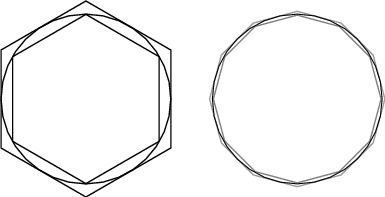
Lo que es inherentemente diferente en estas transformaciones que el 1er 2do producir malos resultados, mientras que el 3º no? Hay alguna heurística que podrían hacer alusión a nosotros cuando la transformación es válida para el cálculo del límite? He leído la discusión sobre mathstackexchange sobre el pi=4, pero todavía no podía conseguir que la intuición. Hay una interesante discusión sobre la divergencia de los derivados de estas dos curvas. Pero todavía no entiendo si es una condición satisfactoria para demostrar que Arquímedes construcción fue una válida.

Si es posible, favor de dar 2 dos explicaciones de la intuición y estrictamente punto de vista matemático.

Answer 1

El punto clave es el menor semicontinuity (y, en general, la no-continuidad) del perímetro cuando aproximada (en cierto sentido, para ser más precisos) de una determinada región $R$ con algunas regiones $R_n$ (por ejemplo polígonos). Tan solo se puede decir en generalque $$ \textrm{Por}(R)\leq\liminf_n \textrm{Por}(R_n). $$ Nada más. Si, por alguna razón, usted sabe a priori que, por cualquier $n$, $\textrm{Per}(R)\geq \textrm{Per}(R_n) $, a continuación, se puede concluir $$ \textrm{Por}(R)= \textrm{Por}(R_n). $$ Este es el caso de la aproximación del círculo con los polígonos inscritos: se postula que la cuerda es siempre menor que la de arco, es decir, la línea recta es la longitud mínima de la curva, por lo $\textrm{Per}(R)\geq \textrm{Per}(R_n) \;\forall n$.

Por supuesto, esto además de la propiedad no se aplican en su aproximación con el exterior polígonos y, de hecho, para esta aproximación $$ \pi= \textrm{Por}(R)<\liminf_n \textrm{Por}(R_n)=\liminf_n 4=4. $$