¿Cuál es la definición exacta y precisa de un ÁNGULO?

Question

En wikipedea he encontrado una definición de Ángulo como tal:

"Para medir un ángulo arco circular centrado en el vértice del ángulo se traza, por ejemplo, con un par de compases. La longitud del arco s se divide entonces por el radio del arco r, y posiblemente se multiplica por una constante de escala $k$ (que depende de las unidades de medida que se elijan): $$\theta = k \frac{s}{r}.$$ El valor de así definido es independiente del tamaño del círculo: si se modifica la longitud del radio, la longitud del arco cambia en la misma proporción, por lo que la relación $s/r$ no se altera".

Y la definición de arco circular se da como:

"un arco de círculo es un segmento de un círculo, o de su circunferencia (límite) si el círculo se considera un disco".

Ahora bien, como el arco de círculo es un segmento de una circunferencia, no podemos tener arcos de longitud superior a la circunferencia del círculo. Por tanto, no podemos definir ángulos mayores que $2\pi$ de esta manera. Pero he encontrado un tema en el libro "Álgebra y trigonometría unificadas" (Addison-Wesley mathematics series) art 3-5. Lo he publicado como respuesta a la pregunta

https://physics.stackexchange.com/questions/87057/angular-displacement/87066#87066 .

Allí el autor del libro explica que podemos tener arco circular más que la circunferencia de un círculo como:
" ....donde el arco circular $\stackrel \frown {PP}^{}$ denotado por $s$ ,.... ya que el número de revoluciones de cualquier ángulo viene determinado por la relación de la longitud del arco circular interceptado $s$ a circunferencia del círculo definimos, magnitud de un ángulo en revoluciones como

Ángulo en revoluciones $ = s/2r$ ..."

significa que puede haber ángulos de más de $2\pi$ .

Pregunta1 :¿Depende la definición de ángulo de su uso en física?

Pregunta2 : si asignamos un punto a un cuerpo sólido llamado $P$ con un ángulo inicial $\theta$ después de que este cuerpo sólido gire un círculo completo, ¿podemos suponer que el ángulo del punto $P$ después de la revolución volver a ser $\theta$ ou $\theta +2\pi$ . Por favor, indique una definición precisa para apoyar la validez de este argumento.

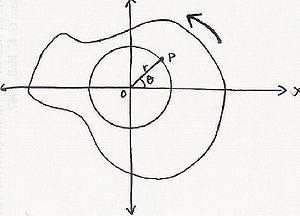Como entiendo si asignamos coordenadas polares para señalar $P$ estas coordenadas polares serán $(\pm r,\theta\pm 2n\pi)$ y pero si se trata de rotación debemos considerar el ángulo utilizado como " orientado " o " no orientado ".

Answer 1

"Ángulo" es un tema delicado. Existen (al menos) las tres interpretaciones siguientes, aplicables según las circunstancias.

(a) La más sencilla es la siguiente: Dados dos vectores distintos de cero ${\bf x}$ , ${\bf y}\in{\mathbb R}^n$ , $\>n\geq2$ El ángulo (no orientado) $\alpha$ entre ellos es el número no negativo $$\alpha:=\arccos{{\bf x}\cdot{\bf y}\over|{\bf x}|\>|{\bf y}|}\in[0,\pi]\ .$$ En particular: Dados dos rayos que parten del mismo punto $P$ en el espacio el "ángulo cerrado $\alpha$ "es un número comprendido entre $0$ y $\pi$ inclusive, y es igual a la longitud del arco más corto recortado sobre el círculo unitario en el plano de estos dos rayos.

Esta idea de ángulo también está en la base de la trigonometría esférica, donde el ángulo entre dos puntos ${\bf u}$ , ${\bf v}\in S^2$ se considera la distancia entre estos dos puntos. Como tal, satisface la desigualdad del triángulo.

(b) Cuando alguna rotación alrededor del origen en ${\mathbb R}^2$ entonces el grupo $SO(2)$ pasos a la acción, y tiene sentido hablar de ángulos orientados . Un ángulo orientado es una clase de equivalencia de números reales módulo $2\pi$ . Cada una de estas clases tiene un único representante en el intervalo $[0,2\pi[\ $ o en el intervalo $\ ]{-\pi},\pi]$ y el conjunto de estas clases está biyectivamente relacionado con $SO(2)$ .

Un ejemplo: El mapa $$T:\quad (x,y)\mapsto(x\cos\alpha-y\sin\alpha,\ x\sin\alpha+y\cos\alpha)$$ es una rotación del plano euclídeo alrededor del ángulo $\alpha\in{\mathbb R}/(2\pi{\mathbb Z})$ . Cuando la rotación se realiza físicamente en el tiempo y todos los puntos giran de hecho en forma de carrusel $n$ vueltas completas antes de parar en el lugar adecuado la información sobre $n$ no está presente en $T$ .

(c) El grupo circular $SO(2)$ tiene la línea real completa ${\mathbb R}$ como su "cobertura universal". A veces es conveniente trabajar en ${\mathbb R}$ al hablar de ángulos, por ejemplo, al estudiar la espiral logarítmica $$\sigma:\quad t\mapsto (e^t\cos t,e^t\sin t)\qquad(-\infty<t<\infty)\ .$$

Otro ejemplo importante es el siguiente: Se tiene una curva cerrada $$\gamma:\quad t\mapsto {\bf z}(t)=\bigl(x(t),y(t)\bigr)\in\dot{\mathbb R}^2\qquad(0\leq t\leq L)$$ que rodea el origen un cierto número $n$ de veces. Para calcular este $n$ acumulamos los cambios infinitesimales de $\phi(t):=\arg\>{\bf z}(t)$ y al final dividir por $2\pi$ . Aquí $\phi(t)$ sólo está "definida hasta $2\pi$ "como en b), pero $\phi'(t)$ está bien definida y viene dada por $$\phi'(t)={x(t)y'(t)-x'(t)y(t)\over x^2(t)+y^2(t)}\qquad(0\leq t\leq L)\ .$$ De ello se desprende que el incremento argumental total $\Delta\phi\in{\mathbb R}$ a lo largo de $\gamma$ viene dado por $$\Delta\phi=\int_0^L\phi'(t)\ dt=\int_0^L {x(t)y'(t)-x'(t)y(t)\over x^2(t)+y^2(t)}\ dt\ ,$$ a partir de la cual obtenemos $n={\Delta\phi\over 2\pi}$ . En análisis complejo este número aparece como $$n(\gamma,0)={1\over2\pi i}\int\nolimits_\gamma{dz\over z}\ .$$

Answer 2

Aunque la respuesta de Christian Blatter es realmente impresionante, para ser sincero, creo que lo está complicando demasiado para el propósito del PO. Para dar una definición precisa de los ángulos en la geometría plana clásica, primero tenemos que distinguir entre el objeto geométrico real y la asignación de un valor al mismo. Así es como me lo enseñó Ravi Kulkarni y creo que disipa una enorme cantidad de confusión y ambigüedad que rodea al tema y con la que un número sorprendentemente grande de matemáticos parecen estar totalmente de acuerdo.

Hay varias maneras de hacer esto--voy a ir con mi versión de Edwin Moise presentación en Geometría elemental desde un punto de vista avanzado . Creo que es la formulación más sencilla en la literatura de libros de texto.

Procedamos como sigue: Primero necesitamos una definición precisa de la "esquina" del objeto geométrico a la que asignamos el número real positivo que llamamos ángulo. Las "esquinas" se producen en la geometría clásica cuando 2 segmentos de línea definidos por 3 o más vértices en el plano se cruzan en un punto final. Tomemos lo siguiente:

Definición: Sea $A$ y $B$ son los segmentos de línea no paralelos definidos por los puntos $a,b$ y $c$ en el plano y que se intersecan en uno de los puntos. Entonces definimos la esquina, o $\angle abc$ como la unión de $A$ y $B$ .

Sencillo y muy preciso. Sin confusiones. Observe que asumimos la unicidad de los segmentos de línea para evitar la ambigüedad sobre qué esquina se define aquí en la elección de la construcción de los puntos finales. Ahora definimos el mapeo de ángulos.

Definición: Sea f: abc -----> R donde R es la recta real y $$0\leq f(abc)\leq II$$ Entonces llamamos f a la función de mapeo de ángulos o de medida de ángulos en el plano.

Ahí lo tienen. Una definición precisa y rigurosa de un ángulo.

Una pregunta interesante: ¿es f realmente un medir en el sentido de la teoría de la integración? La respuesta es claramente negativa, a menos que definamos el mapa de medidas sólo en los reales positivos. Hay buenas razones para no hacerlo en geometría.

Adenda: He editado un poco para aclarar algunas sutilezas. Espero que ahora sea aceptable. Una formulación completamente precisa-con todos los detalles-se puede encontrar en el texto de Moise. Una construcción similar, aunque más complicada, se puede encontrar en el libro de Richard Millman y George Parker Geometría Un Enfoque Métrico Con Modelos .