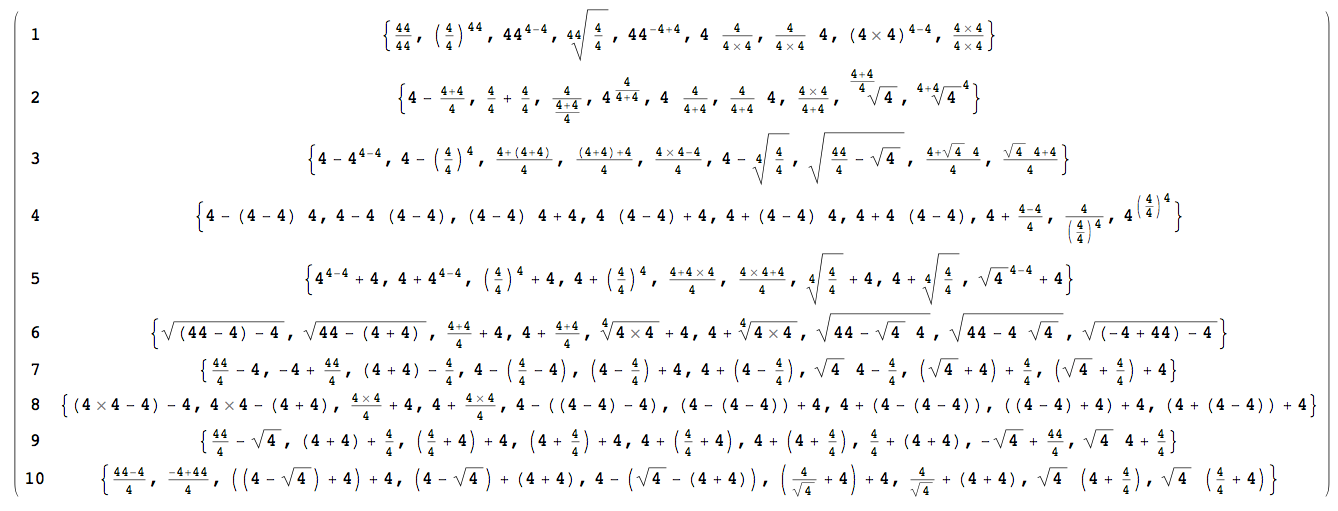Crear una recursividad que utiliza la notación polaca inversa. Aquí es un pseudo-código:
function rec(digitsLeft, numbers, operators, expression):
if digitsLeft == 0 and numbers - operators == 1:
value = evaluate(expression)
if value in {1..10}: output expression
return
if digitsLeft > 0:
rec(digitsLeft - 1, numbers + 1, operators, [expression, 4])
if digitsLeft > 1:
rec(digitsLeft - 2, numbers + 1, operators, [expression, 44])
if numbers - operators > 1:
for op in ['+', '-', '*', '/']:
rec(digitsLeft, numbers, operators + 1, [expression, op])
La notación polaca inversa se encargará de los operadores de prioridad, de modo que usted no tiene que manejar los soportes.
La llamada inicial es:
rec(4, 0, 0, [])
y los parámetros son:
digitsLeft -- ¿cuántos dígitos qué necesidad tenemos ya de uso,numbers -- ¿cuántos números de nuestra expresión ya tiene,operators -- ¿cuántos operadores nuestra expresión ya tiene,expression -- la matriz de la celebración de los elementos de la expresión.
Por supuesto, usted necesita escribir evaluate (la función que evalúa expression) y output (que es la función que lo más probable es convertir la notación polaca inversa expression para el estándar de notación de infijo (usando algunos de los algoritmos conocidos, por ejemplo este) y la impresión a la pantalla o a un archivo).
Una versión más general sería sustituir esto:
if digitsLeft > 0:
rec(digitsLeft - 1, numbers + 1, operators, [expression, 4])
if digitsLeft > 1:
rec(digitsLeft - 2, numbers + 1, operators, [expression, 44])
con un bucle que vaya a través de $4$, $44$, etc., pero para este ejemplo, era más fácil hacer un copiar/pegar de dos if-s.
Si necesita cualquier aclaración adicional, por favor pregunte.