Un resultado conocido como el teorema de Birkhoff prohíbe esférica de la radiación electromagnética. El enunciado del teorema es que cualquier esféricamente simétrica de vacío de la solución a las ecuaciones de Maxwell debe ser estática. Es bastante fácil de demostrar. En un esféricamente simétrica solución de $\mathbf E$ $\mathbf B$ debe ser radial. Hacer un Ansatz, $$\mathbf E = E_0 \exp(i(\mathbf k\cdot\mathbf r-\omega t)) \hat r \quad \mathbf B = B_0 \exp(i(\mathbf k\cdot\mathbf r-\omega t)) \hat r $$
El wavevector $\mathbf k$ debe $\mathbf k = k\hat r$ de simetría esférica.
Ahora la ley de Ampere $$\nabla\times \mathbf B = i\mathbf k \times \mathbf B = 0 = \partial_t \mathbf E = -i\omega \mathbf E$$ which implies $\omega = 0$, so that the field is static, or $E_0 = 0$. From Faraday's law $\nabla\times\mathbf E =- \partial_t \mathbf B$ you can see that if $E_0 = 0$ but $\omega \neq 0$, then also $B_0 = 0$.
La mayoría de los resultado general para la radiación electromagnética es que en el gauge de Coulomb, en la zona de radiación, el vector de potencial es $$\mathbf A(\mathbf x, t) = \frac{\mu_0}{4\pi }\frac{e^{i(kr-\omega t)}}{r} \int \mathbf J(\mathbf x') e^{-ik\hat{x} \cdot \mathbf x'} \, dx'$$
donde $\mathbf J(\mathbf x')$ es la corriente en la región de origen, por ejemplo, la antena, y el actual se supone que sinusoidal (armónica) dependencia del tiempo. [Esto no es una restricción, debido a que las ecuaciones de Maxwell son lineales y la transformada de Fourier existe.]
La dependencia angular está enteramente en la integral sobre la fuente de corriente. Por lo tanto para conseguir algunos deseado perfil angular de la radiación, es necesario diseñar $\mathbf J$ adecuadamente.
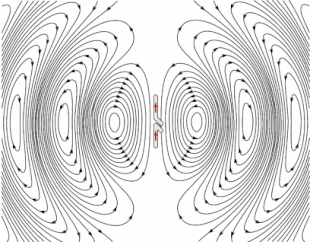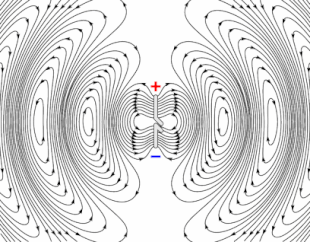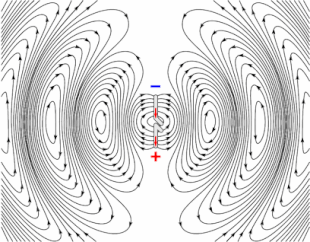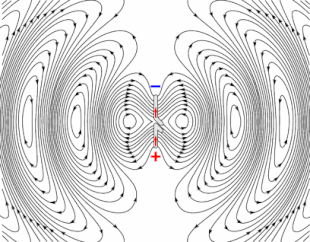
Su caso en particular de un resonador de esfera de carga en realidad no irradia porque sólo tiene un monopolo momento y no hay monopolio de la radiación. Un esferoidal la distribución de carga es tratada por Jackson Electrodinámica Clásica, Seg 9.3. Hay Jackson muestra que esta disposición conduce a cuadrupolo radiación con cuatro lóbulos de distribución de potencia radiada. Para una discusión más detallada, lea Ch. 9 en Jackson, que trata de la radiación en detalle, incluyendo la distribución angular de la potencia radiada a partir de diversas fuentes.