No, la distribución de Cauchy es una distribución muy predecible en el sentido de que los cuantiles están bien definidos. Si conoces $\mu$ y $\sigma$, entonces la probabilidad de ubicación de que una observación aparezca entre dos puntos, de un tamaño de muestra donde $n\to\infty$, está bien definida. Sin embargo, mientras que el 50% de los datos aparecerán en $\mu\pm\sigma$, el 99.95% central de los datos será $\mu\pm{636.62}\sigma$.
Además, $\sigma$ no es una desviación estándar; es un parámetro de escala. No hay media definida, por lo que los momentos superiores tampoco existen. A menudo se dice que la media y la varianza son infinitas y bajo una definición de la integral eso es casi verdad, pero bajo otra comprensión de la integral, simplemente no existen. Puedes pensar en una varianza o una media como una propiedad que algunas distribuciones tienen, pero otras no. Así como las narices son una propiedad de los vertebrados, si ves un árbol con nariz, entonces no es un árbol. Si ves una distribución con varianza, entonces no es la distribución de Cauchy.
La distribución de Cauchy aparece bastante en la naturaleza, particularmente donde hay alguna forma de crecimiento. También aparece donde las cosas giran, como las rocas rodando por colinas. La encontrarás como la distribución central de una fea mezcla de distribuciones en los rendimientos del mercado de valores, aunque no en los rendimientos de cosas como antigüedades vendidas en subastas. Los rendimientos de antigüedades también pertenecen a una distribución sin media ni varianza, pero no a una distribución de Cauchy. Las diferencias son creadas por las diferencias en las reglas de la subasta. Si cambiaras las reglas de la NYSE, entonces la distribución de Cauchy desaparecería, y aparecería una diferente.
Para entender por qué generalmente está presente, imagina que eres un postor en un conjunto muy grande de postores y postores potenciales. Dado que las acciones se venden en una doble subasta, la maldición del ganador no se aplica. En equilibrio, el comportamiento racional es ofertar tu valor esperado. Una expectativa es una forma de media. Una distribución de estimaciones medias convergerá a la normalidad a medida que el tamaño de la muestra tienda a infinito.
Por lo tanto, los precios, si la empresa no va a quebrar o ser comprada en una fusión, se distribuirán normalmente si no hay costo por liquidez (que lo hay). Si la cantidad de acciones no cambia, entonces el rendimiento para invertir en el tiempo t es $$r_t=\frac{p_{t+1}}{p_t}$$. Eso lo convierte en la razón de dos distribuciones normales. Si la integración se realiza alrededor de los precios de equilibrio, en lugar de en (0,0), terminarás con una distribución de Cauchy truncada. Si desagregas los rendimientos en transacciones individuales a lo largo del siglo XX, encontrarás que una Cauchy truncada coincide estrechamente con los rendimientos observados una vez que eliminas fusiones, costos de liquidez y quiebras.
Esto hace que el mercado de valores sea muy volátil, si uno piensa que el mercado de valores debería tener una distribución normal o log-normal, pero no inesperadamente volátil si esperas las colas pesadas.
He construido tanto las distribuciones predictivas bayesianas como las frecuentistas para la distribución de Cauchy y, según sus suposiciones, funcionan bien. La predicción bayesiana minimiza la divergencia de Kullback-Leibler, lo que significa que es tan cercana como puedes estar a la naturaleza en una predicción, para un conjunto de datos dado. La predicción frecuentista minimiza la divergencia de Kullback-Leibler promedio sobre muchas predicciones independientes de muchos muestras independientes. No necesariamente funciona bien, sin embargo, para una muestra individual como se esperaría con una cobertura promedio. Las colas convergen, pero lo hacen lentamente.
La distribución de Cauchy multivariante tiene propiedades aún más perturbadoras. Por ejemplo, aunque obviamente no puede tener covarianza ya que no hay media, tampoco tiene nada similar a una matriz de covarianza. Los errores de Cauchy siempre son esféricos si no está sucediendo nada más en el sistema. Además, aunque nada covaríe, tampoco nada es independiente. Para entender lo importante que eso podría ser en un sentido práctico, imagina dos países que están creciendo y que comercian entre sí. Los errores de uno no son independientes de los errores del otro. Mis errores influyen en tus errores. Si un país es tomado por un loco, los errores de ese loco se sienten en todas partes. Por otro lado, dado que los efectos no son lineales como se esperaría con una matriz de covarianza, los otros países pueden romper relaciones para minimizar el impacto. Corea del Norte es un ejemplo de esto.
Esto también es lo que hace tan peligrosa la guerra comercial de Trump. La segunda economía más grande del mundo después de la Unión Europea declaró la guerra económica a través del comercio contra cada otra economía individual y está financiando esa guerra endeudándose con el dinero para luchar contra aquellos con los que declaró la guerra. Si esas dependencias se ven obligadas a deshacerse, será feo de una manera de la que nadie tenga memoria viva. No habíamos tenido un problema similar desde la Administración Jackson cuando el Banco de Inglaterra embargó el comercio atlántico.
La distribución de Cauchy es fascinante porque aparece en sistemas de crecimiento exponencial y en forma de S. Confunden a la gente porque su vida cotidiana está llena de densidades que tienen una media y generalmente tienen una varianza. Esto dificulta la toma de decisiones porque se aprenden lecciones incorrectas.





9 votos
1. Tu pregunta es vaga / poco clara, por lo que es difícil responder; por ejemplo, ¿qué significa "impredecible" en tu pregunta? ¿a qué te refieres con "las desviaciones estándar de Cauchy" y la convergencia al final? No parece que estés calculando desviaciones estándar en ningún lugar. ¿desviaciones estándar de qué, exactamente? 2. Muchas publicaciones en el sitio discuten propiedades del Cauchy que pueden ayudarte a enfocar tu pregunta. También puede valer la pena consultar Wikipedia. 3. Sugiero evitar el término "forma de campana"; ambas densidades parecen tener aproximadamente forma de campana; simplemente llámalas por sus nombres.
4 votos
Ciertamente, el Cauchy es muy heavy tailed.
1 votos
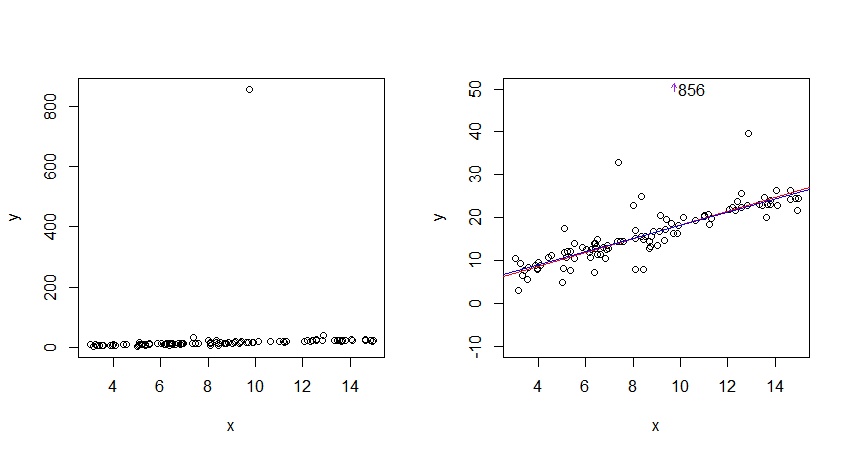
He publicado algunos datos; espero que te ayuden a descubrir lo que quieres saber para que puedas refinar tu pregunta.
1 votos
Al ver tu edición, no estoy seguro de lo que quieres decir cuando dices "¿es posible que las colas de la función de densidad de Cauchy nunca converjan?". Ciertamente, la densidad tiende a 0 a medida que $|x|\to\infty$, y la función de supervivencia también tiende a 0 a medida que $x\to\infty". ¿Podrías aclarar lo que quieres decir?
0 votos
@Glen_b ¿Que nunca alcancen el 0? ¿Que se pueda obtener un "valor atípico de cualquier tamaño", pero con probabilidad cada vez menor? Compara eso, por ejemplo, con el hecho de que la secuencia tiene un índice máximo por el cual converge a 0. Pero si la varianza es infinita, ¿entonces las colas nunca llegan a 0?
1 votos
La densidad normal nunca alcanza 0. Hay distribuciones con colas aún más ligeras que la normal que nunca alcanzan 0.
0 votos
@Glen_b Nunca he visto valores atípicos significativos con
rnormsin embargo. Me pregunto cómo obtenerlos.2 votos
Los valores atípicos grandes son posibles con la normal pero son increíblemente raros. La densidad (y en la cola superior, particularmente de relevancia para valores atípicos de al menos un tamaño dado, la función de supervivencia) para la normal tiende hacia 0 mucho más rápidamente que la Cauchy, pero sin embargo ambas densidades (y ambas funciones de supervivencia) se acercan a 0 y ninguna llega nunca a alcanzarlo.
0 votos
Dado que la distribución de Cauchy no tiene una media y varianza finitas (de hecho, ambas son indefinidas), la media de la muestra no es asintóticamente normal. Sin embargo, existe un comportamiento asintótico útil para la mediana de la muestra; vea por ejemplo aquí.
1 votos
@J.G. De hecho, la media de la muestra es exactamente Cauchy, no es necesario discutir el comportamiento asintótico.
0 votos
@DilipSarwate Énfasis en "útil"; la mediana es aproximadamente Normal, por lo que se puede estimar con una precisión razonable si la muestra es lo suficientemente grande, al igual que los medios de distribución de un ejemplo de TLC de un libro de texto.