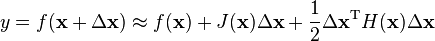Término de la tercera orden en serie de Taylor

Question

¿Qué es el tercer fin de plazo de la Expansión en Series de Taylor? Sé que va a ser de la tercera orden en derivadas parciales, pero quiero saber cómo está expresado en un compacto notación Matricial. Por ejemplo Jacobiana de primer orden, de Hess para los de segundo orden en derivadas parciales.

En otras palabras, ¿qué es el tercer fin de término en la ecuación de abajo? Gracias por su ayuda!

Answer 1

Bien, $f: \mathbb{R}^n \rightarrow \mathbb{R}^n$ ha multivariante expansión de Taylor en $x+h$ centrada en $x$ de los: $$ f(x+h) = f(x)+\sum_{i=1}^n \frac{\partial f}{\partial x_i}h_i +\frac{1}{2}\sum_{i,j=1}^n \frac{\partial^2 f}{\partial x_i\partial x_j}h_ih_j+\frac{1}{6}\sum_{i,j,k=1}^n \frac{\partial^3 f}{\partial x_i\partial x_j\partial x_k}h_ih_jh_k+ \cdots$$ Aquí podríamos definir $T: \mathbb{R}^n \times \mathbb{R}^n \times \mathbb{R}^n \rightarrow \mathbb{R}^n $ por sus valores sobre la base de los elementos de $e_i,e_j,e_k$ (unidad de vectores de base de coordenadas Cartesianas en $n$-dimensiones) $$ T_{ijk}=\sum_{i,j,k=1}^n \frac{\partial^3 f}{\partial x_i\partial x_j\partial x_k} $$ La pregunta es, podemos escribir la fórmula de $\sum_{i,j,k=1}^nT_{ijk}h_ih_jh_k$ como la multiplicación de la matriz de algún tipo... sugiero que considerar la posibilidad de $\mathbb{R}$valores $f$ como punto de partida.

(con la adecuada convenios se establece que hay una manera de escribir esto como una multiplicación de la matriz, pero, creo que en el proceso de hacer tal le pierde la pista de el manifiesto trilinearity, no estoy muy versado en la necesaria notación en este punto en el tiempo, así que voy a dejar mi respuesta aquí tal y como está, ya que expresan esto como una multiplicación de la matriz en un espacio abstracto no es tan interesante, bueno, al menos para mí hoy en día)

Answer 2

Usted puede tomar un vistazo a mi papel en http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2364989. Yo uso una asignación de tensor de la matriz que permite escribir un quinto orden de la serie de Taylor en notación matricial. Tomemos, por ejemplo, el tercer fin de plazo. Si usted tiene un tensor $f_{xxx}$ de las dimensiones de $n\times n\times n\times n$ cuyas $m,i,j,k$ elemento es la derivada de la $m$'th entrada de $f$ respecto de la $i,j,k$ entradas de $x$, puede utilizar el remodelar función para cambiar en una matriz de dimensiones $n\times n^3$. A continuación, $\frac{1}{6}g_{xxx}\left( x\otimes x\otimes x\right)$ es el tercer fin de plazo de la serie de Taylor en notación matricial.