Puzzle de lobos y polluelos

Question

Este problema es del videojuego de mano, El profesor Layton y la aldea curiosa .

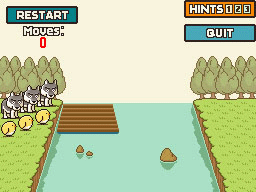
La solución me parece muy chula, pero más que eso, quiero saber cómo demostrar que el número mínimo de movimientos para una solución tiene que ser 11.

También quiero saber cómo encontrar el número mínimo de movimientos en una solución para un número arbitrario de lobos y pollos, donde el número de pollos es mayor o igual que el número de lobos, y los animales pueden comenzar en cualquiera de las dos islas (obedeciendo la regla de que un lado no debe tener más lobos que pollos).

He preguntado a alguien que es licenciado en matemáticas y me ha dicho que se trata de un problema de programación lineal. Pero es una pena, porque yo sólo tengo cálculo de bachillerato en mi haber.

¿Puede explicarme esto?

Answer 1

Cada vez que vayas puedes llevar como máximo 2 animales. Cuando vuelvas, tendrás que llevarte al menos uno. Por lo tanto, después de 10 movimientos como máximo habrás llevado 10 animales en el barco y habrás llevado 5 animales de vuelta en el barco. Por lo tanto, justo antes del undécimo movimiento estarás en el lado inicial del río y tendrás al menos un animal en el lado del río en el que estás. Esto demuestra que no es posible hacerlo en menos de 11 movimientos.

Answer 2

(Demasiado largo para un comentario.) Por cierto, se pueden visualizar todas las jugadas posibles transformando el rompecabezas en un problema gráfico:

El $x$ y $y$ Los ejes representan, respectivamente, el número de pollos y el número de lobos en el a la izquierda lado del río. Las flechas negras significan un movimiento del lado izquierdo al lado derecho, y las flechas rojas representan viajes en dirección opuesta. Comenzamos en $(3,3)$ . El objetivo es alcanzar $(0,0)$ por un camino entrelazado por flechas negras y rojas. No es difícil ver que, de alguna manera, el camino debe contener el subcamino $(3,1)\to(1,1)\color{red}{\to}(2,2)\to(0,2)$ .