Calcular el radio para el diámetro aparente

Question

Fondo

Animar la aproximación a los planetas, como en un viaje a través del Sistema Solar. A una distancia de 2 Unidades de mezcla una esfera llena toda la altura del puerto de vista de la cámara:

Esto genera la siguiente imagen:

Unidades, medidas y distancias

La esfera tiene 4.879,4 km de diámetro, es decir, 1 Unidad de mezcla .

La posición final de la cámara es de 9758,8 km del planeta, o 2 Unidades de mezcla .

La posición inicial de la cámara está a 45999102,0 km del planeta, lo que es demasiado Unidades de mezcla (9427.2).

Problema

Escala el radio del planeta para simular cómo se vería a una distancia determinada de la cámara.

Progreso

El diámetro angular del objeto puede calcularse mediante:

$ = 2 \times arctan( r / D )$

Dónde:

• es el diámetro angular;
• r es el radio; y
• D es la distancia.

Haciendo números:

 = 2 arctan( 2439.70 / 45999102 )
  = 0.0001060759 radians

Actualización nº 1

Creo que puedo usar lo siguiente:

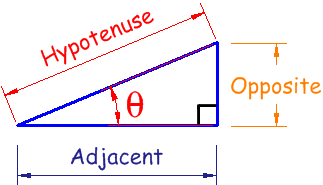
La distancia a la cámara (lado adyacente) es de 9758,8 km.

Desde $tan() = opposite \over adjacent$ entonces $opposite = adjacent \times tan()$ . Así

o = 9758.8 km tan(  )
  = 9758.8 km tan( 0.0001060759 )
  = 1.035 km

Actualización nº 2

Así, a una distancia de 45999102 km, el tamaño aparente de una esfera de 2439,70 km de diámetro sería de 1,035 km a una distancia de 9758,8 km.

Desde el 1 Unidad de mezcla \= 4879,4 km, se deduce que la esfera debe tener un radio de 0,000212116 Unidades de mezcla que es completamente invisible.

Preguntas

1. ¿Me he extraviado?
2. ¿Cuál sería el mejor método para calcular el factor de escala apropiado para el radio de la esfera (en Unidades de mezcla )?

Solución

Usando la respuesta de Henry se obtiene:

• Radio del planeta, $r_p = 2439.7 km$
• Distancia al planeta, $D_p = 45999102 km$
• Distancia Blender, $D_b = r_p \times 4 = 9758.8 km$
• Diámetro aparente: $2r \sqrt{ 1 - r^2 / D^2 }$
• Distancia aparente: $D r^2 / D$
• Factor de escala: $Simulated\space apparent\space diameter \over Simulated\space apparent\space distance$ $\div$ $Blender\space apparent\space diameter \over Blender\space apparent\space distance$

Diámetro aparente simulado = $2 \times 2439.7 \times \sqrt{ 1 - 2439.7^2 \over 45999102^2 }$ = $4879.40 km$

Distancia aparente simulada = $45999102 - 2439.7^2 \over 45999102$ = $45999101.87 km$

Diámetro aparente del mezclador = $2 \times 2439.7 \times \sqrt{ 1 - 2439.7^2 \over 9758.8^2 }$ = $4724.46 km$

Blender distancia aparente = $9758.8 - 2439.7^2 \over 9758.8$ = $3659.55 km$

$\therefore$ Factor de escala = $4879.40 \over 45999101.87$ $\div$ $4724.46 \over 3659.55$ $\approx .0000821660$

Gracias.

Answer 1

Habría pensado que deberías haber δ = 2 arcsin( r / D ) lo que significaría que a medida que la cámara se acerca a la superficie del planeta, $\delta$ se acercaría $\pi$ .

Supongo que sabes dibujar un disco circular de diámetro $2r$ a distancia $D$ en su sistema de animación. A medida que la cámara se acerca al (centro del) planeta, el disco aparente parecerá tener un diámetro de 2 r cos( δ / 2 ) y estar a una distancia de D - r sin( δ / 2 ) .

Puede evitar las funciones trigonométricas utilizando un diámetro aparente de $2 r \sqrt{1-r^2/D^2}$ y una distancia aparente de $D - r^2/D$ .