Intuición detrás de la fórmula para$\sum i^{2}$

Question

He estado tratando de averiguar la intuición detrás de la cerrada de la fórmula:

$\sum i^{2} = \frac{(n)(n+1)(2n+1)}{6}$

Esto no es difícil de demostrar a través de la inducción, así que no estoy interesado en la prueba de que esto es cierto. Más bien, estoy más interesado en por qué alguien podría incluso hacer este cálculo para un paso inductivo. ¿Por qué es tan confuso para mí es que

$\sum i = \frac{(n)(n+1)}{2}$ tiene sentido el uso de la Gaussiana truco de tomar el número de la línea y doblarlo por la mitad y darse cuenta de que (1+n) = (2+(n-1)) = (3 +(n-2))... para terminar con este formulario.

Pero, ¿qué es la intuición para $i^{2}$? Mirando estas dos fórmulas, uno se da cuenta muy rápidamente de que

$\sum i^{2} = \sum i * \frac{(2n+2)}{3}$

Pero, ¿por qué es que la verdadera intuitivamente? ¿Qué es la intuición?

Answer 1

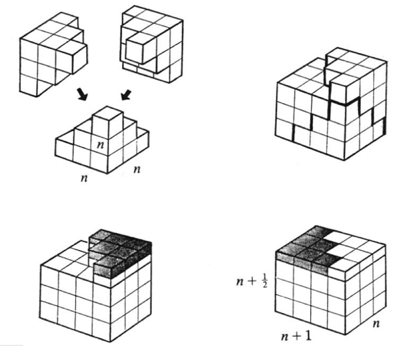
Desde que usted pidió una intuitiva explicación considerar un simple caso de $1^2+2^2+3^4+4^2$ el uso de un conjunto de niños de bloques para construir una pirámide-como la estructura.

Primero organizar $16$ bloques en un $4\times4$ plaza. Lo siguiente que se coloque en la parte superior de esta disposición, $9$ bloques en un $3\times3$ plaza de la alineación de los bloques de la esquina superior izquierda de cada cuadrado, una encima de la otra. En la parte superior de esta construcción lugar de $4$ bloques en un $2\times2$ plaza, de igual forma alineada. Finalmente la corona de la esquina superior izquierda con un solo bloque para el $1\times1$ plaza.

La siguiente tabla representa el número de bloque en cada columna de la disposición visto desde arriba:

$\begin{array}{cccc} 4&3&2&1\\ 3&3&2&1\\ 2&2&2&1\\ 1&1&1&1 \end{array}$

Podemos encontrar el número total de bloques en la disposición sumando el número de columnas que contienen un solo bloque a dos veces el número de columnas que contiene dos bloques, a continuación, la suma de tres veces el número de columnas que contiene tres bloques y, finalmente, la adición de cuatro veces la de una columna que contiene cuatro bloques.

\begin{eqnarray} \sum_{i=1}^4i^2=1\cdot(4+3)+2\cdot(3+2)+3\cdot(2+1)+4\cdot1 \end{eqnarray}

Si hacemos lo mismo con una pirámide de bloques de $n\times n$ bloques en su base, a continuación, la suma sería similar a la siguiente:

\begin{eqnarray} \sum_{i=1}^{n}i^2&=&1\cdot(n+n-1)+2\cdot(n-1+n-2)+3\cdot(n-2+n-3)\\ &+&\cdots+(n-1)\cdot(2+1)+n\cdot1\\ &=&1\cdot(2n-1)+2\cdot(2n-3)+3\cdot(2n-5)+\cdots+(n-1)\cdot3+n\cdot1\\ &=&\sum_{i=1}^{n}i(2n-2i+1)\\ &=&2n\sum_{i=1}^{n}i-2\sum_{i=1}^{n}i^2+\sum_{i=1}^{n}i\\ \sum_{i=1}^{n}i^2&=&(2n+1)\sum_{i=1}^{n}i-2\sum_{i=1}^{n}i^2\\ 3\sum_{i=1}^{n}i^2&=&(2n+1)\sum_{i=1}^{n}i\\ &=&\dfrac{n(n+1)(2n+1)}{2}\\ \sum_{i=1}^{n}i^2&=&\dfrac{n(n+1)(2n+1)}{6} \end{eqnarray}

Answer 2

ps

Tenga en cuenta que he obtenido esto de esta pregunta de Mathoverflow. El autor original es Man-Keung Siu.

Answer 3

Es esto realmente lo bueno llamado triángulo de Pascal. Tal vez usted ha oído hablar de él, y se muestra a continuación;

Usted también puede saber de el Palo de Hockey de Identidad:

Sorprendentemente, el Palo de Hockey de la Identidad puede ser utilizado para casi directamente muestran que

$$\sum_{k=1}^nk(k+1)(k+2)\dots (k+p)=\frac{n (n+1)(n+2)\dots (n+p+1)}{p+2} $$

Véase, pues, que si $p=1,0$, tenemos

$$\sum_{k=1}^nk^2=\sum_{k=1}^nk(k+1)-k=\frac{n (n+1)(n+2)}3-\frac{n(n+1)}2=\frac{n (n+1)(2n+1)}6$$

Me gusta usar esto porque el general suma que implican $p$ puede ser derivada como una combinación de suma dividiendo ambos lados por $(p+1)!$. También pasa a ser fácil de recordar y, en general funciona bien para derivar las fórmulas para $\sum k^a$. Sólo para mostrar cómo iba a funcionar para $k^3$,

$$\sum_{k=1}^nk^3=\sum_{k=1}^n k (k+1)(k+2)-3k (k+1)+k\\=\frac {n (n+1)(n+2)(n+3)}4-3\frac{n (n+1)(n+2)}3+\frac {n(n+1)}2\\=\frac {n^2 (n+1)^2}{2^2} $$

Answer 4

Diferencias una vez que se dan a $i^2$, de nuevo da $2i-1$, y una tercera vez da una constante $2$.

Esto sugiere que la fórmula debe ser de tercer grado del polinomio con los principales coeficiente de $\dfrac{2}{3!}=\dfrac13$ como se podría esperar en el caso de integrar $2$ tres veces.

Por tanto, no es difícil encontrar la solución: una forma es buscar en $\sum i^{2} - \dfrac{n^3}{3}$ y tomar la primera y segunda diferencia para obtener una constante. Al final esto va a dar una inductivo hipótesis de $$\sum_{i=1}^n i^{2}=\dfrac{n(n+1)(2n+1)}{6}$$, que es un error tipográfico lejos de tu pregunta