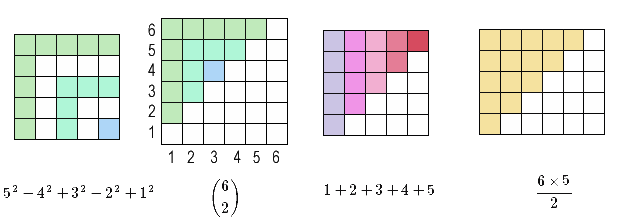Prueba combinatoria de que los coeficientes binomiales se dan mediante sumas alternas de cuadrados?

Question

Un estudiante recientemente preguntó si había una demostración combinatoria de la siguiente identidad:

$\begin{equation*} \sum^n_{k=1}(-1)^{n-k}k^2 = {n+1 \choose 2}. \end{equation*}$

Estaba apurado y no pude encontrar nada bueno en el momento. ¿Alguna idea o imágenes para que esto sea más claro?

Answer 1

Más una prueba visual que combinatoria, tal vez:

$$ 5^2 - 4^2 + 3^2 -2^2 +1^2 = {6 \choose 2}$$

En la izquierda, tienes la suma alternada como inclusión-exclusión de cuadrados: la suma total es el número de celdas coloreadas.

En la derecha, tienes esas formas en forma de L reordenadas en la parte superior izquierda de una cuadrícula de 6x6. Si piensas en cada celda como una coordenada $(x_1,x_2)$ que da dos elementos elegidos del conjunto $\{1, 2 \cdots 6\}$, se ve que los elementos son elegidos con $ x_2 > x_1$, lo que corresponde a una combinación (sin repetición y sin orden).

Agregado: Los otros son bien conocidos, pero, solo por completitud...

$$\displaystyle \sum_{k=1}^n (-1)^{n-k} k^2 = {n+1 \choose 2} = \sum_{k=1}^n \; k = \frac{(n+1) \; n}{2}$$

Answer 2

Des hazte de los signos negativos al unir los dos últimos términos de la suma, luego los dos antes de estos, y así sucesivamente. El resultado es el área de un subconjunto del cuadrado de $n\times n$ formado por cuadrados de $1\times1$ componiendo tiras en forma de L: la tira más grande es la unión de las $n$ columnas y la $n$ línea horizontal, las tiras consecutivas están separadas por tiras similares, cada tira comienza en el eje vertical de coordenadas luego va hacia el este y luego hacia el sur y termina en el eje horizontal de coordenadas, y espero que con estas indicaciones todos puedan imaginar el resultado.

Ahora, colorea en negro las tiras que componen el subconjunto que se quiere medir y colorea en blanco el resto del rectángulo:

$\blacksquare\blacksquare\blacksquare\blacksquare\blacksquare$
$\Box\Box\Box\Box\blacksquare$
$\blacksquare\blacksquare\blacksquare\Box\blacksquare$
$\Box\Box\blacksquare\Box\blacksquare$
$\blacksquare\Box\blacksquare\Box\blacksquare$

Luego, añade una línea blanca de ancho $n$ en la parte superior de la imagen:

$\Box\Box\Box\Box\Box$
$\blacksquare\blacksquare\blacksquare\blacksquare\blacksquare$
$\Box\Box\Box\Box\blacksquare$
$\blacksquare\blacksquare\blacksquare\Box\blacksquare$
$\Box\Box\blacksquare\Box\blacksquare$
$\blacksquare\Box\blacksquare\Box\blacksquare$

El rectángulo resultante tiene tamaño $n\times(n+1)$ y pretendo que esté uniformemente coloreado. Esto demostrará el resultado ya que su área es $n(n+1)$.

Para demostrar esto, se pueden emparejar sub-rectángulos de colores opuestos. El primer par está formado por toda la línea $n+1$ (blanca) y toda la línea $n$ (negra). Bórralas ambas. El rectángulo resultante tiene tamaño $n\times(n-1)$:

$\Box\Box\Box\Box\blacksquare$
$\blacksquare\blacksquare\blacksquare\Box\blacksquare$
$\Box\Box\blacksquare\Box\blacksquare$
$\blacksquare\Box\blacksquare\Box\blacksquare$

Sus dos últimas columnas tienen colores opuestos, bórralas ambas. El rectángulo resultante tiene tamaño $(n-2)\times(n-1)$ y es el rectángulo aumentado que se consideraría para resolver el caso $n-2$:

$\Box\Box\Box$
$\blacksquare\blacksquare\blacksquare$
$\Box\Box\blacksquare$
$\blacksquare\Box\blacksquare$

Continúa estos pasos de borrado hasta el final (donde se obtiene un rectángulo uniformemente coloreado de tamaño $1\times2$ si $n$ es impar y $2\times1$ si $n$ es par) o asume que la hipótesis se cumple en el rango $n-2$, de cualquier manera se ha terminado.

Edit Una alternativa, tal vez más simple, es pelar el rectángulo de $n\times(n+1)$, empezando desde los lados superior y derecho, una forma en L tras otra. Por ejemplo, la primera forma en L es la unión de los $2n$ cuadrados elementales en la última línea y la última columna. Luego el resultado sigue del hecho de que estas formas en L están todas uniformemente coloreadas.

Answer 3

Podemos usar la imagen muy bonita en la publicación de Didier Piau (sin la línea blanca agregada en la parte superior) y contar una historia algo diferente.

Imagina que $n$ es impar, porque así lo hace la imagen. Las cosas cambian apenas si $n$ es par.

Primero (y sin importancia) cambiamos la historia que llevó al coloreado. Invertimos la adición, de modo que estemos viendo $5^2-4^2+3^2-2^2+1^2$. Si este truco "algebraico" no es lo suficientemente combinatorio, podríamos encontrar la manera de evitarlo, pero preferimos no hacerlo.

Por un subsquare de $j \times j$ nos referimos al cuadrado de $j \times j$ con la esquina inferior izquierda la misma que la esquina inferior izquierda del cuadrado original.

Coloreamos el cuadrado completo de negro. Luego coloreamos el subsquare de $(n-1)\times (n-1)$ de blanco, luego el subsquare de $(n-2)\times(n-2)$ de negro, y así sucesivamente. Este proceso de inclusión-exclusión refleja exactamente nuestra suma alternante, y produce el patrón blanco y negro de la imagen.

Luego interpretamos las figuras negras en forma de "L" boca abajo y al revés. Queremos terminar con $\binom{n+1}{2}$.

Imagina elegir $2$ objetos de los números $1$ a $n+1$. Tenemos las siguientes posibilidades: (i) el número más grande usado es $n+1$ o $n$; (ii) el número más grande usado es $n-1$ o $n-2"; y así sucesivamente.

Mira la figura negra en forma de L más grande. Su esquina superior derecha cuenta la elección $\{n, n+1\}$. Los cuadros negros horizontales restantes del L grande cuentan las elecciones $n-1$ elecciones $\{k, n+1\}$ con $k

De la misma manera, la siguiente figura negra en forma de L cuenta la elección de los $n+1$ números, donde el número elegido más grande es $n-1$ o $n-2". Y así sucesivamente.

Answer 4

Por inducción. La fórmula se cumple para $n=0$ porque ambos lados se anulan.

También puedes aumentar $n$ en uno: $$LHS_n = n^2 - LHS_{n-1} = \dots $$ Tuve que agregar el último término $n^2. Sin embargo, los signos de todos los términos anteriores se invirtieron debido al factor $(-1)^n$, así que tuve que agregar un signo negativo delante de $LHS_{n-1}$.

Suponiendo que la ecuación es cierta para $n-1$, es decir, que $LHS_{n-1}=RHS_{n-1}$, la fórmula mostrada es $$ \dots = n^2 - RHS_{n-1} = n^2 - (n-1)n/2 = n(n+1) / 2 = RHS_n$$ lo cual querías que se demostrara.