¿Por qué la longitud de onda afecta la difracción?

Question

He visto muchas preguntas de este tipo pero no pude encontrar en ningún lugar la respuesta a "por qué". Sé que es un fenómeno que se ha visto y descubierto y sabemos que sucede y cómo sucede. Pero mi pregunta es ¿por qué la longitud de onda afectaría la cantidad de difracción? Estoy buscando una explicación lógica muy simple en lugar de una respuesta matemática compleja. ¿Por qué un rayo azul se doblará menos que un rayo rojo a través de una rendija del tamaño un poco mayor que la longitud de onda del rayo azul? Necesito una respuesta que responda "por qué" la difracción depende de la longitud de onda de la luz.

Fuentes de las imágenes: http://www.olympusmicro.com/primer/java/diffraction/index.html

Answer 1

¿Por qué se doblará menos un rayo azul que un rayo rojo a través de una rendija del tamaño un poco mayor que la longitud de onda del rayo azul?

No pienses en la curvatura. Piensa en la difracción de esta manera: si tienes una onda plana incidente en una rendija, entonces puedes pensar en el espacio en la rendija como una línea de infinitos fuentes de puntos que irradian en fase.

Si estás mirando directamente hacia la rendija, entonces todas esas fuentes de puntos están en fase. No hay nada inusual pasando aquí.

Sin embargo, si te mueves un poco hacia un lado, entonces todas esas fuentes de puntos no están en fase. En realidad están en fase, pero como no están a distancias iguales de ti, la radiación de cada una se retrasa por una cantidad diferente. Dependiendo de tu posición, las fuentes de puntos interfieren constructiva o destructivamente, y esto es lo que produce el patrón de difracción.

Si observas de cerca esta imagen, parece que fue generada por una aproximación de cuatro fuentes de puntos en la rendija.

Ahora, la cantidad de estas fuentes de puntos y la diferencia máxima de fase entre ellas, es una función del tamaño de la rendija, obviamente. Si la rendija es más ancha, entonces cuando se ve desde alguna dirección ligeramente descentrada, la diferencia de fase entre la fuente más a la izquierda y la fuente más a la derecha será mayor, porque la diferencia en distancia entre ellas es mayor.

Compara una rendija pequeña:

A una rendija más grande:

¿Se nota la importancia del tamaño de la rendija, verdad?

Bueno, cambiar la longitud de onda es equivalente a cambiar el tamaño de la rendija. Si hacemos la rendija más grande, y hacemos la longitud de onda más grande en la misma cantidad, entonces la diferencia en distancia entre las fuentes es mayor, pero la tasa de cambio en la función de onda es más lenta, por lo que la diferencia de fase entre los dos extremos de la rendija es la misma.

Pero, si simplemente hacemos la longitud de onda más pequeña, y dejamos la rendija igual, la tasa de cambio en la función de onda es más rápida, lo cual es equivalente a hacer la rendija más grande sin cambiar la longitud de onda.

Imágenes de Wikipedia

Answer 2

Mi respuesta será bastante similar a la de PhotonicBoom aunque un poco más gráfica. Cuando se trata de fenómenos de luz, hay diferentes formas de comprenderlos: podemos usar una imagen de onda (Hyugens-Fresnel), podemos usar la imagen más moderna que tenemos (QED) o podemos usar algo un poco más intermedio que es la imagen de los rayos de luz viajando de un punto a otro.

Todos más o menos sabemos que en el aire o el vacío, la luz viaja (sea lo que sea eso) en línea recta desde un punto de origen $S$ hasta un punto de observación $M$.

Esto se deriva del principio de Fermat de la trayectoria más corta seguida por la luz de un punto a otro que puede ser representado por el siguiente dibujo

Ahora, esta imagen de un solo rayo de luz tomando la trayectoria más corta como tal no es suficiente para explicar, hasta donde yo sé, el fenómeno de difracción.

Como dijo alguien en su respuesta, necesitamos tener en cuenta que una teoría adecuada de la luz debería mirar al cuadrado de una amplitud que surge de la naturaleza ondulatoria de la luz.

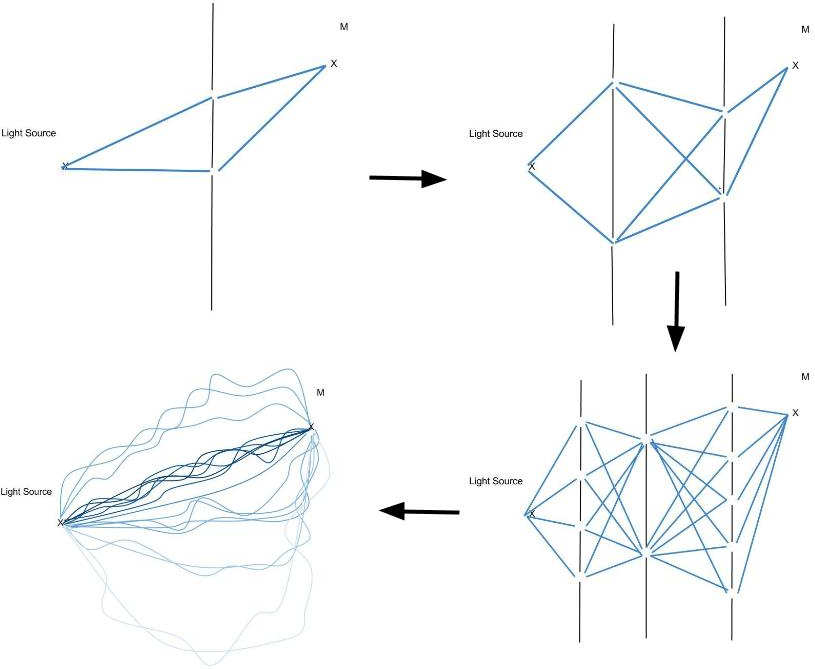
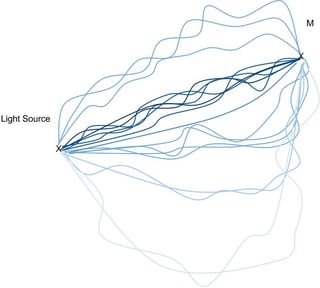
Esto se ilustra con el experimento bien conocido de las rendijas de Young (representado en el panel superior izquierdo de la siguiente figura). Curiosamente, la imagen de los rayos de luz y su longitud óptica sigue siendo muy útil al mirar intererencias y es común representarlas explícitamente de forma gráfica.

Ahora, partiendo del experimento de la doble rendija, se puede intentar añadir otra pared con dos agujeros y ver cómo se ven esas trayectorias de luz (panel superior derecho de la figura 2). Se puede agregar otra pared e incluso más agujeros en esas paredes y seguir observando por qué caminos se tendrían que sumar para obtener la intensidad total de luz en el punto M. Eventualmente, continuando este proceso de añadir paredes y llenar (densamente) con agujeros, se encuentra que necesitamos sumar sobre un número infinito de trayectorias de luz como se representa en el panel inferior izquierdo de la figura 2 incluso en el límite donde ya no hay pared.

Por lo tanto, para explicar la difracción con una imagen de rayos de luz, se necesita imaginar que la intensidad recibida en el punto M es en realidad la suma de las intensidades que provienen de un número infinito de rayos de luz que vinculan el punto de origen con el observador un poco como en la siguiente imagen (versión más grande de una imagen en la figura 2)

Aquí lo que sucede es que la suma de todas las trayectorias está ponderada de tal manera que las trayectorias que están cerca de la más corta tienen un peso enorme y las trayectorias que tienen una longitud óptica muy larga tienen un peso muy pequeño en la suma total (he tenido en cuenta estos pesos aclarando los colores a medida que las longitudes de las trayectorias se hacen grandes). Por lo tanto, en el aire o el vacío la intensidad total recibida se debe abrumadoramente a esas trayectorias que están cerca de un comportamiento en línea recta y se recupera el principio de Fermat.

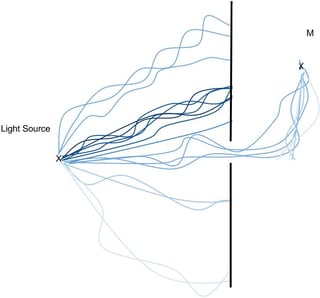
Ahora, ¿qué pasa cuando pongo una pared con un agujero en ella?

Más o menos lo que se muestra aquí

Vemos que en este caso, todas las trayectorias que solían contribuir mucho a la intensidad ya no se pueden usar y solo aquellas que pasan por el agujero permanecen; de ahí la difracción.

Esto sucede para todas las frecuencias de luz para las cuales este agujero no es opaco por alguna razón (su tamaño es demasiado pequeño en comparación con la longitud de onda o algo así). Sin embargo, cuando se trata de la noción de longitud de la trayectoria de viaje (relacionada con el peso que se le da a cada trayectoria dentro de la suma), resulta que depende de la longitud de onda de la luz de tal manera que para la misma trayectoria seguida por la luz, el peso asociado a ella será menor para el color azul que para el rojo, por lo tanto, el color rojo puede llegar más lejos que el azul para el mismo tamaño de agujero.

Aquí van dos/tres comentarios:

• Esta descripción no es incorrecta, creo, pero no es hiper rigurosa

• Está en su mayoría inspirada en una cita en el libro de Zee (QFT in a Nutshell) y en la descripción que Richard Feynman hace de este fenómeno en QED, es solo que yo creo que este fenómeno en realidad no tiene nada que ver con QED y debería ser posible una descripción clásica (basada en rayos de luz).

Los comentarios y las preguntas son muy bienvenidos para mejorar esta respuesta.

Answer 3

El principio de Huygen por sí solo no responderá tu pregunta, sin embargo el principio de Huygen-Fresnel modifica esto para incluir la longitud de onda. Afirma que cada punto en un haz no obstruido actúa como una fuente secundaria de ondas con la misma longitud de onda que la onda primaria. La amplitud del campo óptico en cualquier punto es entonces la superposición de todas las ondas. La superposición tiene en cuenta tanto la amplitud como la fase de la luz.

En tu diagrama los valores de intensidad oscilan y obtienes un pico cuando las ondas se interfieren constructivamente y un valle cuando las ondas se interfieren destructivamente. Considera las dos ondas que vienen de cada borde de la rendija. Cuando impactan en la pantalla habrán recorrido una distancia $d_1$ y $d_2$ respectivamente. Ambas distancias dependen de la posición en la que estás midiendo la intensidad en la pantalla. La diferencia de fase entre las dos ondas es entonces $\phi=(d_1-d_2)*2*\pi/\lambda$. Obtendrás un pico en la intensidad cuando $\phi=0, 2\pi,4\pi, \ldots$ e interferencia destructiva cuando $\phi= \pi, 3\pi, 5\pi \ldots$

Es la interferencia de las ondas, que depende de la longitud de onda, la que causa la dependencia de la longitud de onda en el patrón de difracción.

Para más información busca la difracción de Fraunhofer a través de una sola rendija.

Answer 4

La respuesta se encuentra en QED y es bastante complicada matemáticamente. Como explicación simple, esto es lo que sucede:

Los fotones siguen todos los caminos posibles desde la fuente hasta la pantalla y cada camino tiene su propia amplitud de probabilidad asociada. Sumando todos estos caminos se cancelan la mayoría de los términos en la suma y terminas con tu camino final "clásico" deseado.

El camino depende de la longitud de onda y, por lo tanto, los fotones de diferentes longitudes de onda tienen diferentes puntos finales en la pantalla. No soy un experto en QED, así que alguien con más conocimientos puede ampliar sobre esto.

Consulta el enlace de Wikipedia aquí

Answer 5

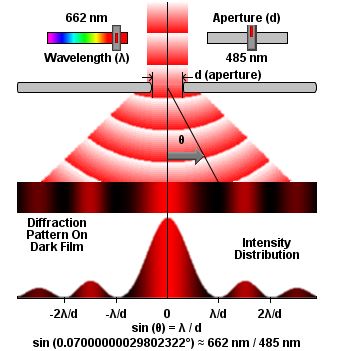
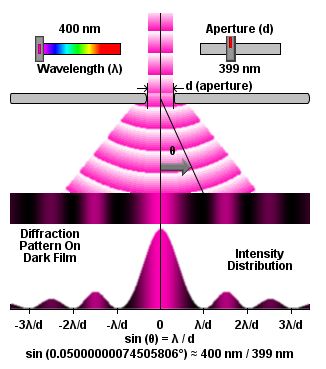
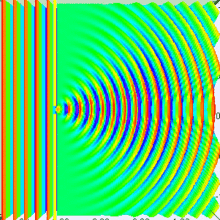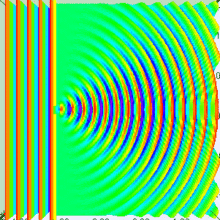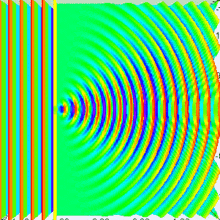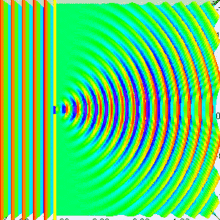
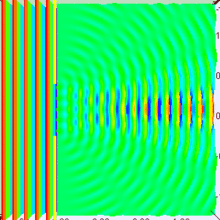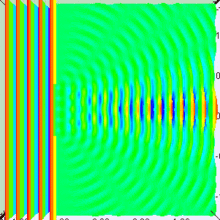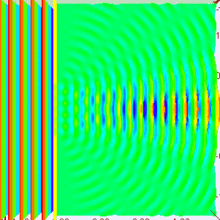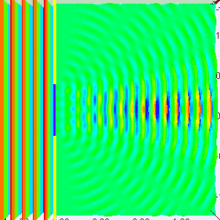
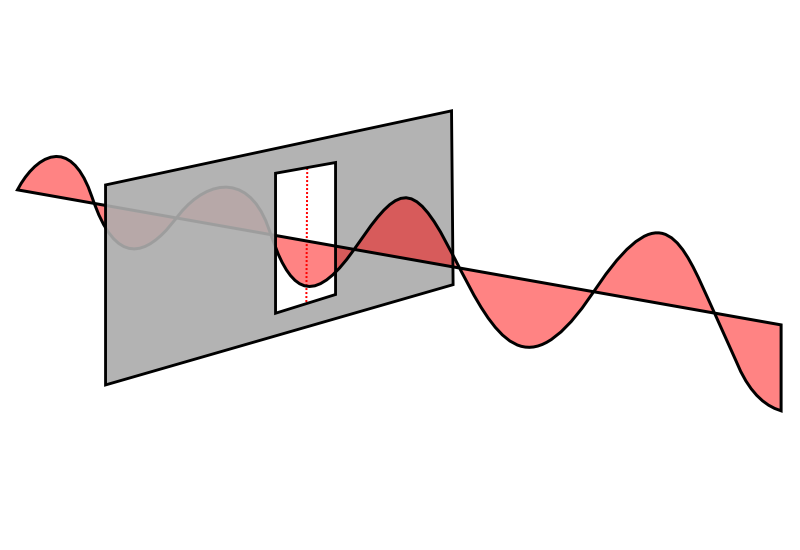Hay muchas respuestas buenas aquí, pero creo que agregaré algunas imágenes que muestran las formas en que tengo que forzarme a pensar para mantenerme al tanto de las diferencias entre las ondas de luz y los rayos de luz al pensar en los patrones de difracción. Arriba tenemos un poco de luz que atraviesa el centro de la rendija. Si lo dibujamos así, parece tener sentido con algunas de las cosas que nos dicen sobre la luz, pero más o menos solo cuenta a medias dos historias distintas. Está dibujado para que parezca una onda (con amplitud, longitud de onda, etc.) pero atraviesa directamente (como un rayo), así que confunde lo que está sucediendo. Si mantenemos en mente estas deficiencias, podemos seguir trabajando.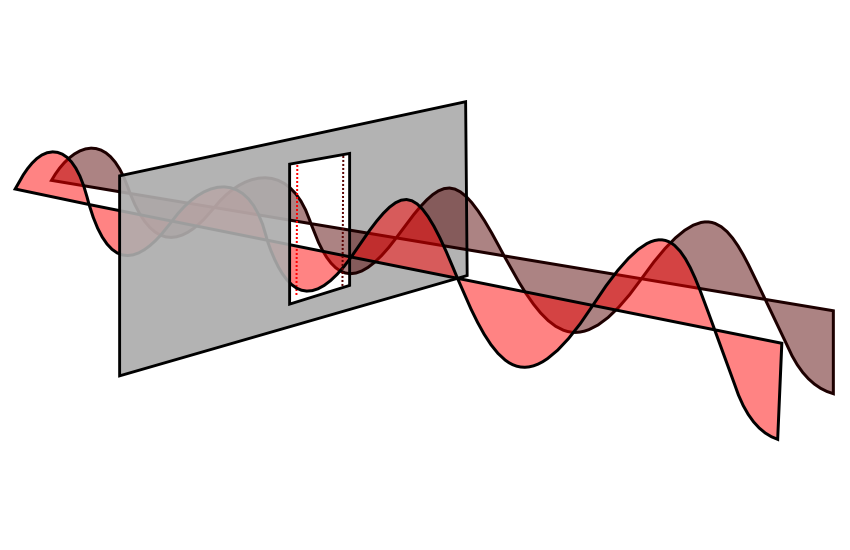

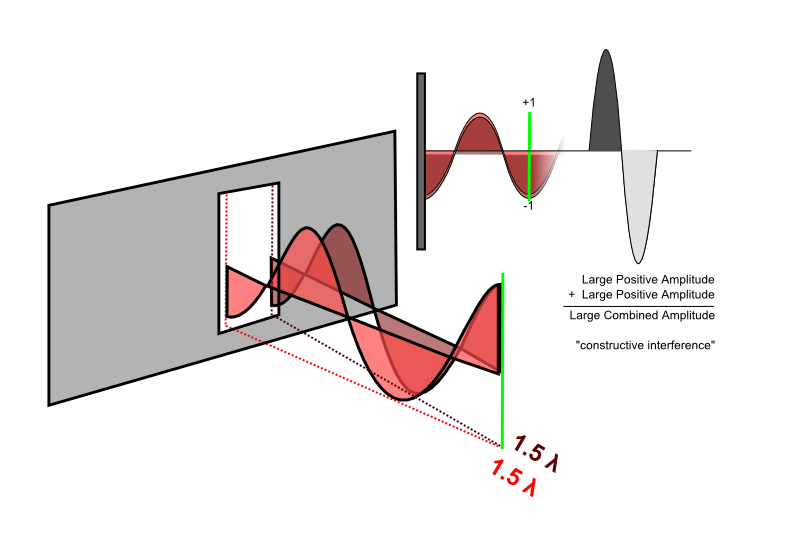
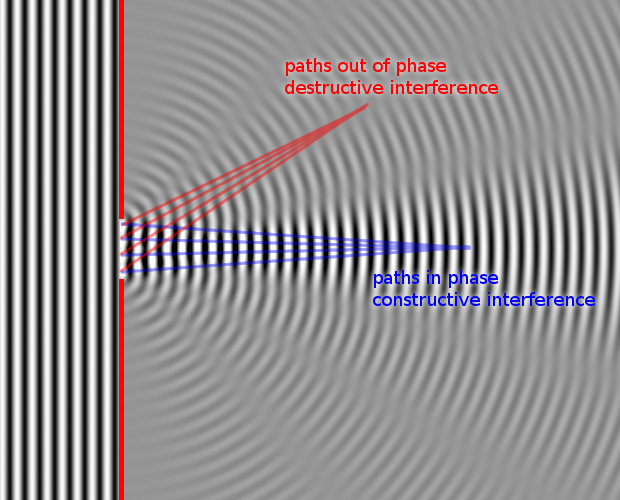
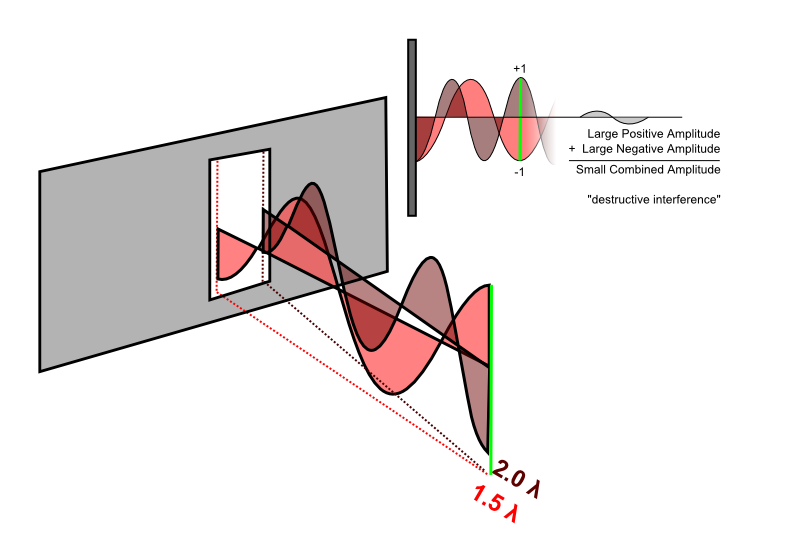Si agregamos más rayos, obtenemos una imagen que parece tener cierto sentido intuitivo; parece que tenemos más luz que atraviesa y donde hay más luz es más brillante la pantalla, ¡pero esa intuición es muy incorrecta cuando tenemos rendijas muy pequeñas! Si hacemos eso, estamos ignorando por completo las propiedades ondulatorias de la luz, ¡y estamos ignorando por completo al pobre Huygens!

Si queremos hacerle justicia a Huygens, tenemos que pensar en muchos puntos actuando como "emisores secundarios" e imaginar cómo múltiples ondas provenientes de múltiples puntos interactuarán más lejos de la rendija.

Si imaginamos dos puntos emitiendo desde cada lado de la rendija e investigamos qué sucede si miramos directamente frente a la rendija, podemos observar un par de cosas. En primer lugar, debido a que estamos mirando un punto justo en el centro frente a la rendija, eso significa que el punto está a la misma distancia de los dos emisores. En el dibujo, esa distancia es de 1,5 longitudes de onda. Debido a que las ondas tienen la misma longitud de onda y recorren la misma distancia, sabemos que las crestas y los valles de la onda se alinearán al llegar a la línea verde. Ya que las ondas se alinean, están "en fase", se suman y forman una onda con el doble de amplitud. El dibujo muestra una onda en blanco y negro para que coincida con los colores de los picos y valles en las imágenes ya publicadas por Phil Frost. Recuerda, las ondas de luz se mueven, como en los dibujos animados, así que no debemos imaginar el blanco como puntos brillantes y el negro como puntos oscuros en el patrón de difracción. Estas áreas con alto contraste en blanco y negro cercanas significan que tenemos grandes amplitudes, ¡por lo que estas áreas grandes y rayadas serán los puntos brillantes! ¿Qué sucede si miramos un punto diferente? Bueno, si ese punto no está a la misma distancia de ambos emisores que estamos imaginando, entonces es posible que ya no estén "en fase" cuando lleguen a la línea verde. De hecho, en el dibujo una onda es baja y la otra es alta, están muy en fases opuestas. Si sumamos dos ondas en fase opuesta, se cancelarán entre sí. Esto crea una onda combinada con una amplitud muy pequeña. Cuando se dibuja en blanco y negro, esto se vería todo gris y descolorido, por lo que eso significa que las áreas grises en esa otra imagen deben ser los puntos oscuros.

Realmente no deberíamos detenernos en uno o dos emisores pequeños, pero se vuelve más difícil de pensar. La imagen realmente se acerca cada vez más a la realidad si agregamos más y más puntos. Podemos pedirle a una computadora que intente hacer todos los cálculos, o podemos hacer un poco de matemáticas y tomar límites para $N=\infty$ emisores y hacer el cálculo para integrar el resultado de todas esas ondas que se suman.

Las cosas que debemos recordar son que los "puntos brillantes" que veríamos en la pared al hacer un experimento de difracción de una sola rendija corresponden a áreas de alto contraste con gran amplitud del dibujo en escala de grises. Además, la luz de una sola longitud de onda no "dobla" al igual que todos los emisores secundarios siempre están emitiendo esféricamente en todas direcciones todo el tiempo; la razón por la que los "puntos brillantes" cambian de lugar es porque cambiar la longitud de onda cambia el número de picos y valles para los viajes desde ambos emisores, y si sus fases ya no están en fase, entonces la luminosidad tiene que cambiar en esa ubicación.

Creo que estos son algunos puntos comunes en los que las personas suelen tropezar al combinar las ideas de ondas, rayos, patrones de difracción y patrones de interferencia. Así que espero que ayude a alguien.

Si tu pregunta era más con la esperanza de obtener una respuesta a "¿por qué incluso el vacío puede actuar como uno de los emisores secundarios imaginarios de Huygens?", entonces supongo que mi respuesta no ayuda en absoluto.